Teaching Engineering Problem Solving

with Mathcad and the Web

 

William Mueller, Philip J. Pritchard

Mathsoft, Inc. / Manhattan College

 

 

Abstract

 

Students often have difficulty understanding basic engineering procedures because of the gulf of mathematical analysis that lies between the definition of a problem and the implementation of its solution.  We describe a new Web-based introduction to engineering problem solving intended to address this difficulty. Using Mathcad as a computational engine, analytic details in the course are selectively de-emphasized, directing student attention to the essentials of problem formulation and interpretation. The approach integrates Mathcad's many pedagogical advantages with the accessibilty, flexibility, and richness of the Web.

 

I. Introduction: The MathSoft Learning Site

The ubiquity of the World-Wide Web has brought both new opportunities and new concerns to the teaching of the undergraduate engineering curriculum. Indeed, the Web has forced a re-examination of the curriculum itself. Using the Web has some obvious advantages—in terms of availability, inter-connectivity, and access to rich sources of data and reference information. On the other hand, spurious and distracting content, and the difficulties of integrating open-ended instructional options into established classroom practice, make effective use of the Web a continuing challenge. Teachers are looking for workable strategies.

With this in mind, MathSoft, the makers of Mathcad software, have launched a Web-based educational resource center called The Learning Site. It is located at:

http://learning.mathsoft.com

The goal of The Learning Site is to provide teachers of engineering, science, and mathematics with reliable, ready-made solutions to the problems of teaching with technology. The site offers online training in the use of Mathcad, as well as integrated collections of learning materials that make use of Mathcad and the Web to deliver their content through engaging, technologically-informed presentations.

Figure 1. A Web page from the MathSoft Learning Site.

Mathcad itself is well known to engineers as an easy-to-manipulate tool for everyday problem solving. Mathcad’s user interface allows regions of text, equations, numerics, and graphics, as well as regions connected to external applications, to be arranged freely on the page. The inter-connectivity of the various regions is also freely arranged, resulting in a creative computing environment that can be shaped to reflect thought processes, metaphors of knowledge construction, and organizational goals. Mathcad’s ability to hide or bypass selected intermediate computations provides a natural way to highlight important cause-and-effect relationships.

These features make Mathcad ideal for engineering design work, but practiced teachers will recognize the pedagogical value of a computing environment that can be adapted to individual learning styles and focus student attention on essential information. Used in a Web-based setting, Mathcad can also be used to direct external resources into rich, integrated learning experiences.

II. Engineering Problem Solving

Almost all engineering problems involve, among other steps:

1)    Applying a theoretical model.

2)    Solving the resulting equations for the unknown or unknowns.

3)    Interpreting the results.

The intent of most of the textbooks used in engineering courses is to focus on items 1 and 3.  (See, for example, Fox & McDonald¹, 1998, in fluid mechanics; Beer & Johnston², 1992, in solid mechanics.) A typical textbook chapter explains the theory and then presents several solved examples, describing the results obtained in the context of the theory.

 

A surprising amount of any given textbook, however, is actually devoted to item 2. Students reading a fluid mechanics book to learn, say, how to solve for the flow in a system of pipes, are often forced to devote a large part of their mental resources to, e.g., solving non-linear differential equations. All too often, the detailed mathematical analysis obscures the problem’s essential physical mechanics, interrupting important cognitive connections between theory and results. Worse, difficult symbolic and numeric computations discourage students from pursuing the “what-ifs”’ that are the basis of independent thought experiments and engineering design. This imbalanced emphasis is especially marked in many textbook exercises. 

 

Working with Mathcad can redress these tendencies. Engineering Problem Solving with Mathcad, a new online collection of integrated case studies on the MathSoft Learning Site, is intended to do just that. The course provides teachers and students with a model of Web-based instruction that focuses on engineering content. The target audience for the course is undergraduates, though graduate students could also benefit from the technologically-informed presentation of engineering problem solving techniques.

 

The course introduces Mathcad as a modeling environment, and students are taken through four separate modeling scenarios:

• Determining the flow from a water tower through a pipe system.
  
  
• Analyzing the design characteristics of a building's modern "tent" roof.
  
  
• Modeling vibrations in a three-mass system with springs.
  
  
• Calculating the deflections in a loaded cantilever beam.

 

Each case study includes a careful formulation, a Mathcad implementation, and a discussion of the engineering implications. Necessary Mathcad features are reviewed in context. Links to relevant Web resources are provided as needed.

The following example contrasts a traditional problem solving approach with the pedagogy employed in Engineering Problem Solving with Mathcad.

Example

“A water tower and standpipe are 10 ft tall. They are connected via a standard elbow to a horizontal pipe 20 ft long and 1 in diameter. The pipe is made of cast iron with a roughness ratio of 0.005. The pipe has an angle valve at the end. Determine the rate of flow (gpm) through this pipe.”

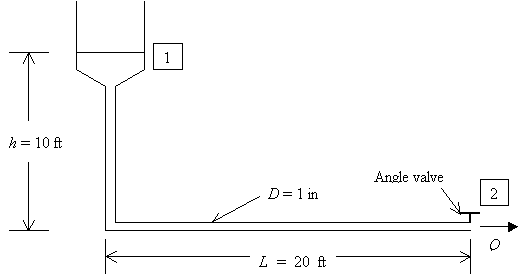
Figure2. Flow from a water tower.

The traditional approach to solving this problem is to first set up the energy equation:

 

(1)

Known quantities here are g, z₁, z₂, L, D, L_valve, L_elbow and K_ent. Unknowns are the velocity V and the friction factor f, which depends non-linearly on V via the Reynolds number Re = rVD/m:

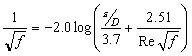
(2)

Students often pause at this point because they have to solve a coupled set of non-linear equations, (1) and (2), to solve for the velocity V and friction factor f.

In the traditional approach^1,3, the student is expected to iterate (either manually or using specialized software), as follows: Make an educated guess for V, compute Re and then f using Eqn. (2); use this f in Eqn.(2) to get a new value of V; repeat until convergence. This approach is tedious, and often quite frustrating for the student. In addition, it is difficult to appreciate the influence of parameters, such as the affect of the pipe diameter on the velocity.

In Engineering Problem Solving with Mathcad, the number-crunching is moved into the background. As students progress through the browser-based instruction, they are presented with numerous opportunities to download related Mathcad worksheets. Students are encouraged to adapt the worksheets, changing data and parameters to test engineering concepts. A section of a Mathcad worksheet from late in the pipe flow case study looks like this:

Figure 3. A Mathcad worksheet focusing on formulation and interpretation.

Once the model has been formulated, Mathcad solves the mathematical problem quickly. Students may then focus on obtaining real-time feedback related to design conjectures.

After completion of the course, students will have been exposed to several classic engineering problems, and have had the opportunity to perform many “thought experiments” to test their knowledge and understanding of engineering science. In doing so, they may overcome their hesitancy about tackling real-world problems that typically involve complicated calculations.

Fundamentally, the course is designed to teach students how to use Mathcad to solve problems by doing.  There are two clear benefits:

 

ü      Students learn how to effectively incorporate technology into their problem solving.

ü      Students are encouraged to explore the “what-ifs” that make general principles real.

 

III. Teaching with Web-based Learning Materials

 

Engineering Problem Solving with Mathcad, like all courses on the MathSoft Learning Site, integrates the computational power and flexible layout of Mathcad with complementary aspects of the Web.

 

Within the Learning Site’s online environment, students read course material, write and save notes, participate in lesson discussions, work through activities and interactive exercises, and evaluate their progress with graded on-line tests. Hints, questions, reviews, links to external information, and the exploratory nature of the Mathcad worksheets themselves create an arena in which students can freely experiment with their understanding of the material. Each lesson offers guidance along a central thread, but there is sufficient supplementary content to let every student find their level, their pace, and points of reference that will relate to their own interests. They can do all of this accordingly to their own schedule, location, and interest level. Many learning styles are accommodated by the non-linear structure and the richness of the integrated environment.

 

Most importantly, however, Learning Site courses free teachers to do what they do best: Teach! Learning Site materials are essentially modular. This means that teachers and students are never forced into a program of instruction that does not suit their needs. They may pick and choose among lessons within a course, subtopics within a lesson, and individual worksheets within a subtopic without breaking any pre-programmed notion of how to proceed. Teachers pick and choose materials as they need them, and shape classroom time accordingly.

 

While modular, Learning Site materials are nevertheless fully integrated. This means that however a student or teacher chooses to use individual pieces, they can count on different materials speaking to one another in a unified voice. Students presented with material from the course in a classroom setting, or those proceeding through the materials on their own, learn to appreciate the connections within the subject while looking at key concepts in many ways.

 

Teachers give Learning Site materials appropriate context and meaning, without having to create the basic building blocks on their own. The materials free teachers to give students individual attention as they work through the mechanical aspects of a subject and consider the feedback that they are receiving. In this classroom model, students learn not only their subject, but the confidence that comes with mastering the technical tools necessary for future success.

 

 

CALL FOR AUTHORS: Engineering Problem Solving with Mathcad is the first offering in what MathSoft hopes will be a wide selection of educational materials for undergraduate engineering instruction. Writing these materials requires qualified authors with experience teaching their subject and a genuine interest in the opportunities presented by online learning. If you might be interested in writing materials for the MathSoft Learning Site, please contact the first author.

 

 

Bibliography

1. Fox & McDonald, Introduction to Fluid Mechanics, 5^th Ed. New York: Wiley, 1998.

2. Beer & Johnston, Mechanics of Materials, 2^nd Ed. New York: McGraw-Hill, 1992.

3. White, Fluid Mechanics, 4^th Ed. New York: McGraw-Hill, 1999.

 

 

WILLIAM MUELLER is Mathematics & Education Specialist at MathSoft, Inc. in Cambridge, MA. He received his undergraduate degree at MIT and his PhD at Duke, both in mathematics. He has been involved in national efforts to develop technology-based instruction for many years. Further information is available at http://www.wmueller.com. He can be contacted at wmueller@alum.mit.edu . Write for a review account on any Learning Site course.

 

PHILIP J. PRITCHARD is an Associate Professor in Mechanical Engineering at Manhattan College, where he is Director of Freshman Engineering. He received his B. Tech. at the University of Bradford (UK), an M.S. at SUNY Stony Brook, and an M. Phil. and Ph.D. at Columbia. His main interests are now in the area of engineering education. In recent years he has specialized in the use of computer software in teaching engineering analysis, in particular the use of Mathcad and Excel. Further information is available at http://www.engineering.manhattan.edu/mechanical/faculty/pritchar.html. He can be contacted at ppritcha@manhattan.edu.