Discovering Differential Equations in Optics

Click here to download this file as a Word document.

William Mueller
Dept. of Mathematics
University of Arizona
Tucson, AZ 85721
mueller@math.arizona.edu

Richard Thompson
Dept. of Mathematics
University of Arizona
Tucson, AZ 85721
rbt@math.arizona.edu

One of the challenges of teaching a truly "reformed," context-based course in calculus or differential equations is finding interesting applications which lead naturally to the consideration of traditional topics. In this note, we outline a multi-part project for investigating two simple problems in geometric optics. Both problems, if pursued, lead students to the study of differential equations with homogeneous coefficients. Individual components of the project, however, are easily adapted to the sophistication of students at lower levels.

An old problem (as old, at least, as Diocles ¹) is to show that the curve which reflects parallel rays of light through a single focal point must be a parabola. We begin an investigation of this problem by giving students a hands on, "manipulative" feeling for it: mounting a shaving mirror on a camera tripod, marking a focal point on the wall, and shining a flashlight on the mirror from above. As a class, we move the tripod around, adjust the mirror so that the reflected ray hits the focal point, and take down some rudimentary data on the slope field which will govern the curve. Students get the idea, but quickly grow restless with the plodding inaccuracy of the method.

As a next step, we ask students to construct an interactive computer page such as the one shown in Figure 1. The idea is exactly the same, but it is apparent that the technology allows them to collect accurate data on the slope field much more efficiently.

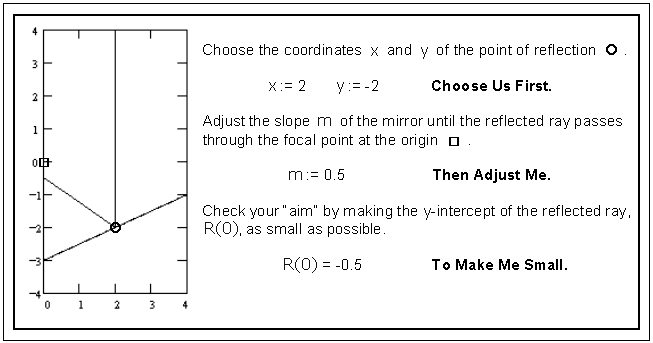
Figure 1. An interactive computer page. (source code)

The page shown (written in Mathcad with most of the operative code off-screen) is easily created in a variety of commonly available platforms. Students make use of the page by first entering the coordinates of one of the lattice points in the displayed half-plane. A slope is then entered, and the program draws a straight line through the chosen lattice point with the chosen slope. Simultaneously, the program draws a vertical incident ray to the lattice point and also a reflected ray that obeys the law of reflection (equal angles) for a planar surface with the given slope. The students can then see how close the reflected ray comes to the origin, and the reflected ray's residual y-intercept is displayed numerically. By adjusting the slope and observing the residual, the students can find the "correct" slope for the curve at that lattice point to any degree of accuracy. The data collection now has some of the appeal of a video game, with students challenged to improve their initial aim at each new point.

As the students go from point to point, their "correct" slopes are entered into a large matrix such as the one shown in Figure 2.

Figure 2. A numerical slope field.

Notice that the central column of the matrix, representing the vertical axis of the curve, would have to be filled in with all zeros. Likewise, the horizontal axis through the origin must contain slopes of ± 1. The entries m_xy to the right of the central column are filled in directly from the student's observations of the "correct" slope at the corresponding lattice point (x, y). Because of the symmetry of the curve, the matrix must be anti-symmetric about the central column, and the left-hand columns can be filled in accordingly. The net result is a matrix which is essentially a numerical slope field for the differential equation governing the desired curve.

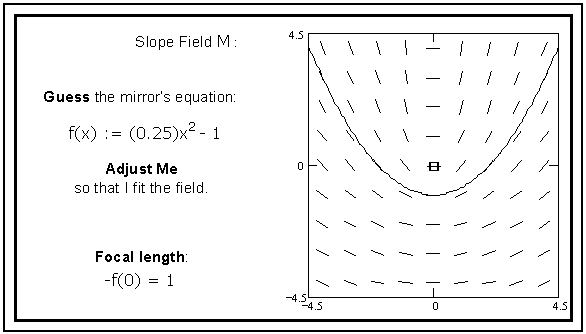
On another working page, the slopes entered as matrix elements m_xy are plotted at each of the lattice points (x, y), showing a more traditional slope field (Figure 3).

Figure 3. Experimenting with solutions. (source code)

On this page, the students interactively experiment with solutions f(x) to the differential equation, and the guesses are plotted through the displayed slope field. With each guess, the students can judge how well the proposed solution fits the slope field that they have found, and they can adjust the function's gross features accordingly. The focal length (the distance between the y-intercept of the guess and the origin) is displayed, and the students are thus able to see that there is a whole family of solutions of different focal lengths, opening wider as the focal length increases. (Here we have displayed a correct "guess." Students are not expected to find exact solutions at this stage, however, or recognize them as exact if they do.)

Students will now have developed an intuitive understanding of many important aspects of the problem: the simple physical law that shapes the differential equation, the geometric connection between the slope at a point and the value of a solution's derivative there, the field of derivatives given by the differential equation, and the qualitative features of the family of integral curves that pass through that field. Having developed this intuition numerically and graphically, students are able to appreciate both the value and the limitations of these representations, and they are ready to see an analytic formulation leading to an exact solution.

It isn't difficult to discover the differential equation describing the field of planar mirrors. Even precalculus students should be able to find a formula for the "correct" slope at a point (x, y). It requires nothing more than a simple diagram and a combination of elementary trigonometry and the Euclidean distance formula.

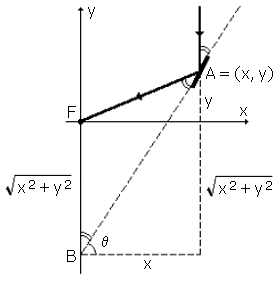
Figure 4. Discovering the differential equation.

In Figure 4, the law of reflection gives equal angles at A and B in the triangle AFB. Since the triangle is isosceles, the two sides FA and FB must be equal, and FA = = FB is the distance from F to A. The required slope m_xy at A is then given by the tangent of the angle q :

When x = 0, it is clear that m_xy = 0. Precalculus students may also be able to "guess" (in Figure 3) that the solutions through the field are parabolas of the form y = ax² + b. They should then be able to adjust the parameters in the equation and obtain a manipulative feeling for the vertical shifts and stretches shaping this family.

Differential equations students, on the other end of the spectrum, can now investigate numerical solutions of the equation y′ = m_xy and compare these with their best guesses in Figure 3. To find the solutions explicitly, the equation may be treated as one of the homogeneous coefficient type ². For x > 0, the change of variable y = zx leads to the separable equation

A table of integrals or any symbolic engine can be used to evaluate the resulting integral

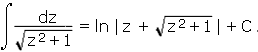
Algebraic manipulation then leads to the solution y = [1/(4f)]x² - f, where y(0) = -f. The same solution is obtained for the case x < 0.

The traditional approach to this problem, in too many textbooks, has been to write down the differential equation (often through some torturous series of diagrams), roll up one's sleeves and integrate, and then declare the problem "solved" when the explicit solutions appear. Used exclusively, this approach does little to develop student's graphical and numerical understanding of the differential equation. The wider approach outlined above leads students to consider the problem from many different points of view. The net result is a much more memorable encounter, and one which builds skills that are of more general applicability to other problems.

To follow up on calculus or differential equations student's analytic understanding of the problem, and to connect the problem to realities outside of the classroom, we ask them to find the equation of the best circular approximation to the parabola at its vertex. Spherical mirrors are much less expensive to manufacture than parabolic mirrors, and most small mirrors of long focal length are made with cross-sections that are circular approximations to the optimum parabolic shape. Finding the correct circle for a given focal length (radius 2f) involves matching the y-intercept and the first and second derivatives of the circle with those of the parabola at the vertex.

Whether students have found an analytic solution to the problem or not, the effects of a spherical approximation can be displayed graphically. Figure 5 shows the results of reflections off the circle rather than the parabola. Focusing errors (aberration) are displayed numerically.

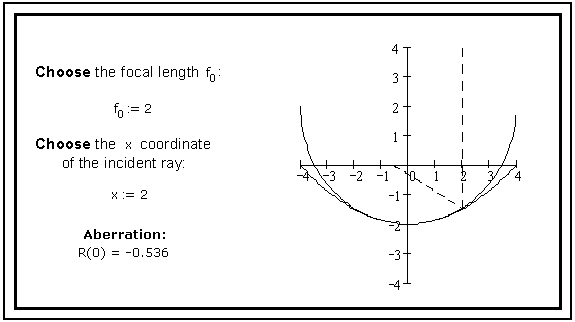
Figure 5. Spherical aberration. (source code)

There is a variation of this problem which can be set up in much the same way, and which leads to some nice complementary geometry. Imagine that the parallel light rays incident on the curve obey not the law of reflection, but rather the law of refraction (Snell's law) as they pass through it. That is, think of the curve as a mathematical idealization of a simple lens rather than a mirror, with a focal point inside of the lens—as when light is focused on the bottom of a shallow pool. (Practically, of course, most lenses involve two refractions, at both a front and a back surface; but we have found that consideration of this second refraction, at least in an initial formulation of the problem, obscures the important mathematical points unnecessarily.) What form would the curves have to take in order to focus the rays at the origin once again?

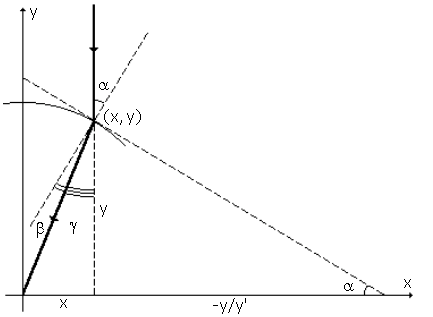
It is instructive, in this case, to proceed by a slightly different route. Using the student's familiarity with the analytic formulation of the reflection problem, we begin by finding the differential equation which governs these curves. Beware, however: the natural formulation of Snell's law in a diagram such as Figure 6, sin a = k sin b, leads to some difficult trigonometry when attempting to convert to the variables x, y and y′. Working instead with a and g, and writing sin a = k sin (a - g ) = k [sin a cos g - cos a sin g ], or 1 = k [cos g - cot a sin g ], leads to triangles in a and g which are much more tractable, as shown in the figure. (It is useful to withhold this secret for a little while, however, to let students struggle with their trig identities.

Figure 6. Refraction.

With the right set-up, Snell's law is quickly converted to

which is once again a differential equation of the homogeneous coefficient type. Making a change of variable and separating, a trig substitution leads, in this case, to the integral

If the student recognizes that the numerator of the integrand is exactly the opposite of the derivative of the denominator, then the integration can be carried through to its finale, yielding curves of the form

k²x² + k²y² = y² + 2cy + c².

Manipulated into the equivalent form

Ax² + B(y - C)² = D,

these curves are recognizable as ellipses (B > 0 or k > 1) and hyperbolas (B < 0 or k < 1).

We think the above analysis speaks for itself—very few students will be able to carry it out completely without being given many hints. The lesson, regardless of how far they proceed, is that looking for an analytic solution is not always the preferred approach; and finding an analytic solution is not always the final word. Many students hold on tightly to the idea that graphical and numerical approaches are mere diversions before the "real" solutions are revealed analytically. They are usually willing to reconsider after an experience like the one above.

Fortunately, there is another way to proceed—one that again brings graphical and numerical methods into play. Students may, e.g., find the differential equation, recognize it as the homogeneous coefficient type, change variables, separate, and get stuck on the integration or its follow-through. What can they do? They must remember what they have learned from the mirror problem. 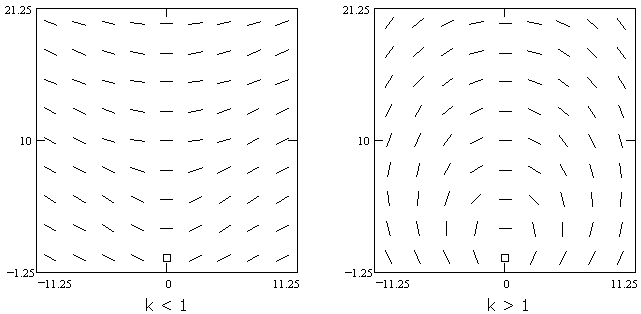Plotting slope fields, for the two cases k > 1 and k < 1, gives something like Figure 7.

Figure 7. Slope fields for focusing refractive curves.

Many students are able to make an educated guess that the integral curves through these slope fields are hyperbolas and ellipses. (Needless to say, many other students will not recognize these curves. Considered team assignments, and careful hints, are usefully employed here.) Students can then review (or learn) the focal equations for these conics. Differentiation shows that they do indeed satisfy the differential equation. The differentiation, and its reduction to the form of the differential equation, are difficult exercises for some students, but they are easy in comparison with the integration outlined above. Finding the circular approximations to the curves, in this case, provides further practice with realistic (ugly) differentiation ³.

In some sense, the point of these investigations has very little to do with optics, or even differential equations, per se. The point is to have students appreciate the many approaches available to them as they struggle with a realistic problem, to see both the value and the limitations of each of these approaches, and to see the way in which the various approaches interact. The above outline, then, is really meant as more of an example of how such a presentation can be achieved effectively. Creative instructors will find ways to do similar things with each of the applications their classes consider.

Acknowledgments. Part of the material in this paper was developed at a workshop sponsored by the Consortium for Ordinary Differential Equations Experiments (CODEE) and funded by the National Science Foundation. The authors would like to thank the referees for several helpful suggestions.

Footnotes

¹On Burning Mirrors; ca. 200 BC.

²Of the form y′ = M(x, y)/N(x, y), with both M(λx, λy) = λⁿM(x, y) and N(λx, λy) = λⁿN(x, y) for some n. These equations provide a nice transition from the study of separable equations to the study of linear equations. Analytically, they are treated exactly like linear equations, with the change of variable y = zu leading to a separable equation. In this case, however, the integrating factor is always just u = x.

³A symbolic processor again works well here.