| Click here to download this file as a Word document. |
Centers of Triangles of Fixed Center:
Adventures in Undergraduate Research
William Mueller
Department of Mathematics
University of Arizona
Tucson, AZ 85721
1. Introduction
There are many popular misconceptions about undergraduate research projects in mathematics: that they are only for advanced students; that they require a tremendous amount of extracurricular time and effort; that they must be guided by an advisor with a vast and detailed knowledge of the subject; that good topics, simultaneously rich and accessible, are difficult to find. The truth is much simpler. The joys and frustrations of mathematical research can be experienced in any subject, at any level. One must only learn to look closely, with an openness to the possibility of discovery.
And "looking" is easier than it has ever been before. Fast computers and friendly software allow students to manipulate their intuitions with a naturalness that most research mathematicians only dreamed of during their own undergraduate days. In the new age of electronic Surrealism 1, students may wander freely through the landscape of mathematics, finding their own way to "advanced" destinations that were previously inaccessible to them. Moreover, and more importantly for the development of undergraduate research projects, it is now possible for students to stop along the way and scrutinize the objects in the landscape in all of their extraordinary detail. The computer, when guided by a genuine curiosity, is capable of revealing "neglected associations" in even the simplest of things. The research advisor, on journeys such as these, need only act as a gentle chaperon, reminding students that the "control exercised by reason" (look carefully and systematically; write down what you see; prove it) is the key to turning their adventures into legitimate mathematical formulations.
2. Motivations
The investigation described here was suggested by some initial computer explorations carried out by students in a multivariable calculus class. Although the results of the investigation are of interest in themselves (in fact, despite their provenance in a subject that has been explored for centuries, I believe that the results are essentially new), we also mean to present the process of the investigation, as an example of how naturally an undergraduate research program may develop. The topic of the investigation comes along in the course of other studies and, at least initially, the investigation is an elementary extension of those studies. Careful, systematic observation, however, reveals the topic's beautiful, unexpected complexities.
Early on in multivariable calculus, students must be introduced to vectors. Before vectors are used to describe something else, which is itself new to students (such as space curves), it is instructive to use them in a more familiar setting. Force vectors are a traditional choice for this—intuitive if not always familiar—and their applicability is readily accepted. This ready acceptance comes at a price, however. The algebra of force vectors is so elementary that the notation's powerful simplicity is obscured.
The advantages of vector notation are much more apparent in another familiar setting: plane geometry. What most undergraduates seem to remember about this subject, from their high school experience, is a tortuous series of theorems and corollaries, and not a great deal of actual geometry. Presented with vector methods, however, the theorems of high school geometry take surprisingly simple form. Expressed elegantly and succinctly by the notation, the geometry itself becomes apparent.
The principal idea of vector-based proofs is to replace selected line segments in geometric figures with vectors, and then substitute the unifying notions of scalar multiplication and (vanishing) dot product for the sundry Euclidean propositions on parallel and perpendicular lines, respectively. For example, consider the theorem that says that the medians of a triangle are concurrent. If such theorems are proved at all in high school texts, they are usually treated algebraically, as a demonstration of analytic geometry, or, alternatively, as a kind of grand crescendo at the end of the text, in which all of the previous propositions are allowed to blow their horns. A tribute to the rigors of mathematical reason, in either presentation, but the geometry is usually lost. By vector methods, the proof is more straightforward:
THEOREM. The medians of a triangle are concurrent.
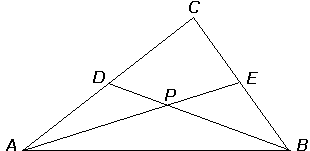
Two medians.
Proof. Let medians AE and BD meet at P, as in Figure 1. Then for some scalar s,
| P |
= A + s AE
= A + s (E - A) = A+ s (((1/2)(B + C)) - A) = (1 - s) A + (s/2) B + (s/2) C . |
For some scalar t,
| P |
= B + t BD
= B + t (D - B) = B+ t ((1/2) (A + C)) - B) = (1 - t) B + (t/2) A + (t/2) C . |
Equating the two expressions for P, we find s = t = 2/3. So P = (1/3)(A + B + C). By the symmetry of this expression, we see that each pair of medians would lead to the same intersection. ¤
Not only is the concurrence immediately apparent in this proof, but the fact that it occurs at a trisection point of each of the medians seems to come for free. The notational advantages displayed in such proofs are much more impressive than any of the vector demonstrations that, for example, two people can pull a car out of the mud. Usually, in fact, a certain number of students (often the ones with the most painful memories of high school geometry) are impressed enough to want to do more; to see what other theorems can be proved this way. At which point the advisor-to-be smiles gently.
3. Questions and Answers
Readers of this Magazine were reminded, in [1], that there are, in fact, many interesting linear triples associated with a triangle, meeting at many other centers. The center where the medians meet is called the centroid of the triangle. Other classic centers include the orthocenter, where the altitudes are concurrent; the incenter, where the angle bisectors are concurrent; and the circumcenter, where the perpendicular bisectors of the sides are concurrent. That each of these centers exists is easily proved with vector methods, and these proofs make good follow-up exercises to the theorem presented above.
Perhaps the most basic question about these centers is this: where do they lie? That is, if one considers triangles of many different shapes and sizes, what is the locus of a particular center? It isn't difficult to demonstrate that, allowed arbitrary rotations and dilations of a triangle (without translation), any of these centers can be made to fall at any point in the plane—a less than marvelous result. Still, the question remains interesting for specific natural classes of triangles, such as those for which one of the centers is held fixed. In this case, the results are indeed quite marvelous.
We will consider two such classes: triangles of a fixed incenter and triangles of a fixed circumcenter. These particular classes are chosen because the auxiliary existence of a fixed incircle or circumcircle, respectively, leads to a parametrization of each class that is especially simple. For each of these two classes, we will consider the locus of the remaining three centers listed above.
Triangles of fixed incenter. How does one consider, e.g., all triangles of a fixed incenter? Similar triangles obtained through rotations and dilations generate only copies of the essential loci, differing in orientation and in scale, and so it suffices to consider triangles with a unit incircle and a base AB parallel to the x-axis, as in Figure 2.
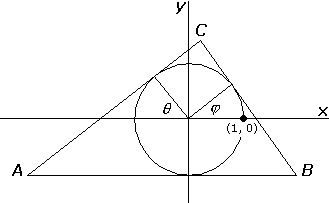
Triangles of fixed incircle.
This class may be parametrized by the two angles q and j , measured upward from the x-axis, giving the inclination of the sides AC and BC, respectively. To assure that the sides meet at C, we will need to restrict the parameters to q Î (-p/2, p/2) and j Î (-q , p/2). A discretization of this domain in the q j - plane, for q and j both between -p/2 and p/2, is shown in Figure 3.
| j |  |
| q |
Domain of triangles of fixed incircle.
Each point in this domain represents a particular triangle with its incenter at the origin. For purposes of computation, the domain must be treated discretely; but, of course, the mesh size may be varied to obtain arbitrary detail (at the cost of increased computation time).
In order to find the other centers of the triangles in Figure 3, it is first necessary to express the coordinates of the triangle's vertices in terms of the parameters q and j . This is another good vector exercise, involving parametrization of the three lines representing the sides, followed by a computation of the intersections by solving the resulting systems of equations. A symbolic processor, such as Maple, is useful for the latter task 2. The results, referring to Figure 2, are:
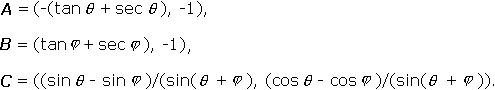 |
It is instructive to plot these vertices as q and j step through the domain at equal intervals, as in subsequent computations. The plot is shown in Figure 4, together with the corresponding edges of the triangles.
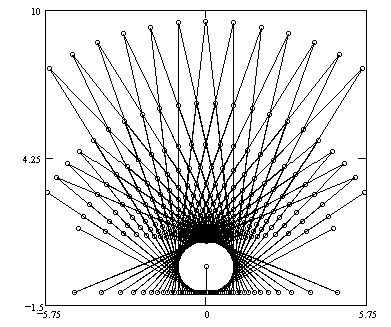
FIGURE 4
Vertices of triangles of fixed incircle.
We see that, for equal increments of the parameters, the triangles themselves do not fill the plane uniformly. Technically, the transformations we consider from the q j -plane to the xy-plane will not be linear ones. We will keep this in mind when examining later plots.
Before considering other centers, a good limbering-up exercise is to compute the values of a more familiar function of q and j : the area. Using vector algebra to determine the base and the height, we find
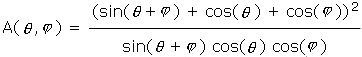
![]() .
.
This surface, and its contours, are plotted in Figure 5 over the domain of Figure 3.
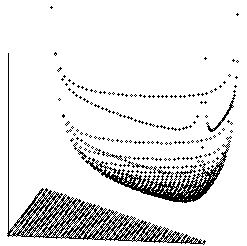 |
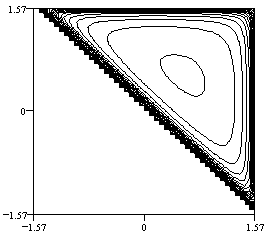 |
Areas of triangles of fixed incircle.
There is an obvious minimum, which occurs when q and j are both p/6. This result should be familiar to anyone who has worked the exercises in old calculus books: the triangle with fixed incircle of minimum area is equilateral.
Centroids. Now let us return to the centroid, the point at which the medians are concurrent. The medians have already been expressed in terms of the vertices, in the proof that we gave above, and computing the coordinates of the centroid at P amounts to finding the value of either of the parameters s or t at the point of intersection, exactly as in the proof. Pedagogically, it is nice that, for each of the centers we consider, the proof of existence provides just such a method of computation. In the case of the centroid, it is great fun to have a symbolic processor strenuously compute the solution to the system of equations in s and t for medians given in terms of q and j, only to have it finally announce that q and j have disappeared and s = t = 2/3, which we already knew (but may have forgotten).
With this information in hand, we can then ask the computer to step through the domain in Figure 3, plotting the centroid for each of the triangles in the class. The result is spectacular:
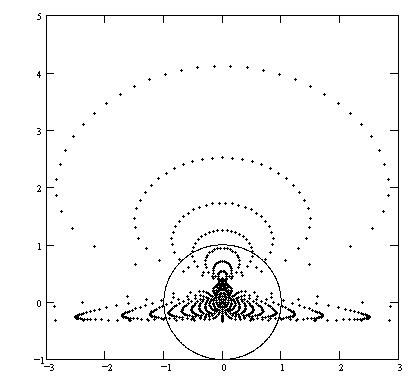
FIGURE 6
Centroids of triangles of fixed incircle.
The circle shown is the incircle. The complexity of this figure seems to persist at smaller mesh sizes and greater resolutions. Apparently, the centroids fall only within a very specific region of the plane, the boundaries of which are far from obvious. Providing an accurate description of this region, or of the curves of constant q and j, would make an interesting research project, although it is by no means clear what level of mathematical sophistication would be required.
Orthocenters. Computing the loci of other centers while the incenter is held fixed produces equally intriguing results. Consider, next, the orthocenter, the computation of which involves the solution of a similar system of equations.
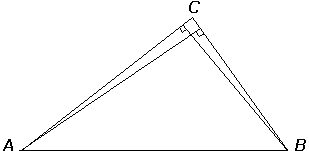
FIGURE 7
In this case, we parametrize lines whose direction must have a vanishing dot product with the direction of other lines. The resulting system of equations is predictably not pretty, but it may be solved, once again, with the aid of a symbolic processor (followed by the requisite checking and simplification). The results are plotted in Figure 8.
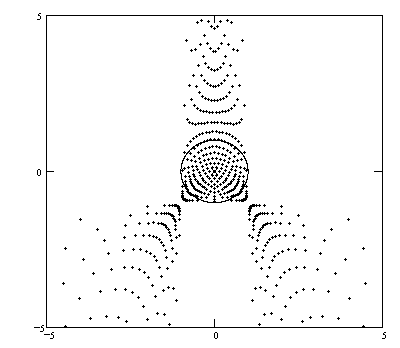
FIGURE 8
Again, the centers appear to be confined to a region of the plane with unknown boundaries.
Circumcenters. We save for last the problem whose statement contains the most appealing balance of Euclidean yin and yang: circumcenters of triangles with a fixed incenter. As Figure 9 shows, this problem is computationally similar to the problem of the orthocenters.
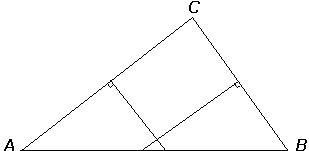
FIGURE 9
Computing the circumcenter.
The resulting locus is shown in Figure 10.
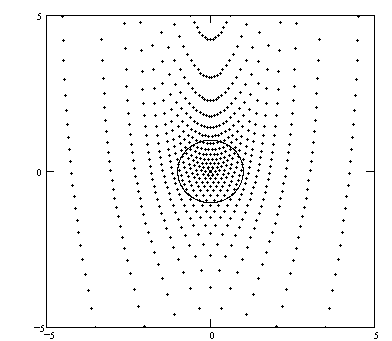
FIGURE 10
Triangles of fixed circumcenter. Investigating the class of triangles with a fixed circumcenter presents no new difficulties; in fact, the parametrization of this class is a bit simpler. As before, it suffices to consider triangles with a unit circumcircle and a base AB parallel to the x-axis. The members of this class are conveniently described by the angle q and the intercept b shown in Figure 11.
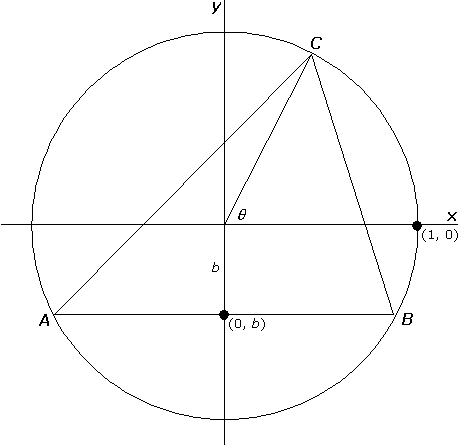
FIGURE 11
A discretization of the parameter domain is shown in Figure 12 for q between 0 and 2p and b between -1 and 1.
| b | 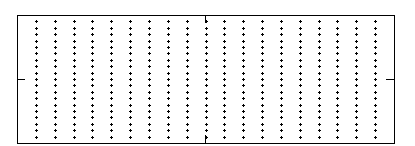 |
| q |
Domain of triangles of a fixed circumcenter.
The coordinates of the vertices are:
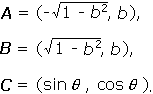 |
A plot of the areas of these triangles, given by
![]() ,
,
is shown in Figure 13.

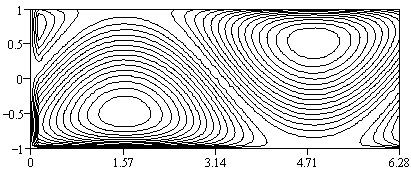
Figure 13
The two equilateral triangles in the domain produce the maximum areas. Notice, as well, the hollow that snakes around the peaks, corresponding to the two q 's that will lead to zero area for any b.
Centroids, orthocenters. Taken together, the plots of the centroids and the orthocenters are quite striking in this case:
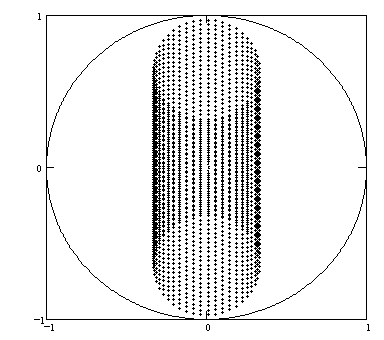
FIGURE 14
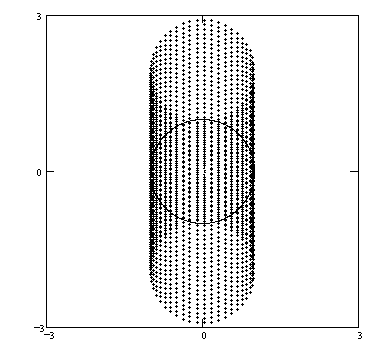
FIGURE 15
The circumcircle is shown in each plot, without which the two would be indistinguishable (except for scale). Apparently, the centroids fall only within the central third of the circumcircle, and the orthocenters fall within a diameter on either side. Surely, theorems await here.
Incenters. Finding the incenters for this class offers a new computational challenge: we must parametrize lines whose direction from two other lines is at equal angles. The dot product will again allow us to describe this situation, but the resulting system of equations is more complex than in any of the previous cases.
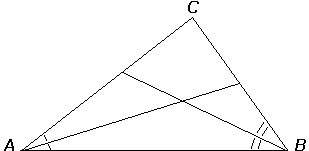
FIGURE 16
After much clicking and whirring, the computer produces Figure 17.
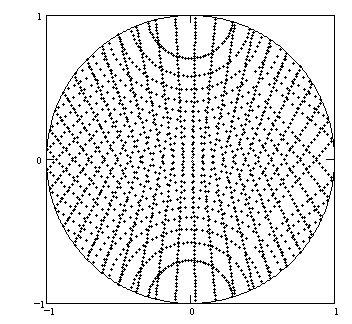
FIGURE 17
We close with the observations of a student of fixed points, who was seen lingering thoughtfully at the International Surrealist Exhibition in London in 1936.
| At the still point of the turning world. Neither flesh nor fleshless; |
| Neither from nor towards; at the still point, there the dance is, |
| But neither arrest nor movement. And do not call it fixity, |
| Where past and future are gathered. Neither movement from nor towards, |
| Neither ascent nor decline. Except for the point, the still point, |
| There would be no dance, and there is only the dance. |
T.S. Eliot, Burnt Norton |
Acknowledgments
The author wishes to thank Betty Mayfield, the editor, and the referees for many helpful suggestions.
Reference
1. C. Kimberling, Central points and central lines in the plane of a triangle, this Magazine, 67 (1994), 163-187.