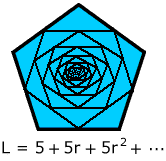 Series, like sequences, come in both arithmetic and geometric varieties.
Series, like sequences, come in both arithmetic and geometric varieties.
Arithmetic & Geometric Series
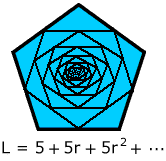 Series, like sequences, come in both arithmetic and geometric varieties.
Series, like sequences, come in both arithmetic and geometric varieties.
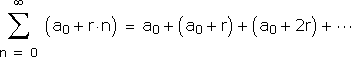
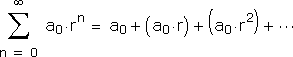
Thus, the series:
is arithmetic with is geometric with It isn't difficult to calculate the respective partial sums. For arithmetic series:
We proceed from the third to the fourth line above by way of a useful formula for the sum of the first N positive integers.
The sequence of partial sums for an arithmetic series grows without bound whenever Geometric series are another matter. Notice that:
So:
Taking the difference gives us:
From this we may solve for the partial sum:
In this partial sum, the only term dependent on N is r N + 1 . When
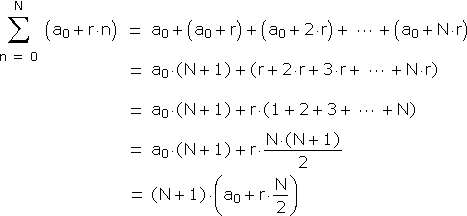
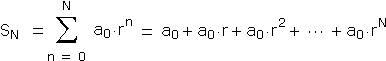
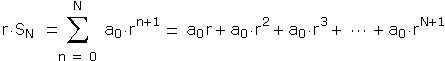
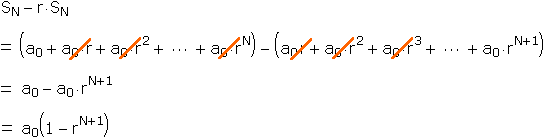
![]()
![]()
![]()
![]()
Back to Contents