The Fundamental Theorem of Algebra
|
Theorem: A polynomial of degree n can have at most n distinct real roots. |
The usefuleness of the Fundamental Theorem comes from the limits that it sets. At most tells us to stop looking whenever we have found n roots of a polynomial of degree n . There are no more.
For example, we may find – by trial and error, looking at the graph, or other means – that the polynomial
Since the polynomial has degree 3, we would be wasting our time looking for others.
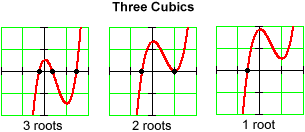
Having at most n roots, of course, is no guarantee that a polynomial will actually cross the x-axis this maximum number of allowable times. For example, the cubic polynomial
The possible number of roots between 0 and n depends on how we count.
If we count distinct roots (as we usually do), then:
|
A polynomial of even degree can have any number from 0 to n distinct real roots.
|

This is of little help, except to tell us that polynomials of odd degree must have at least one real root.
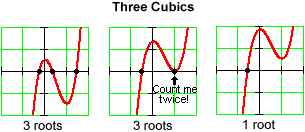
If we count roots according to their multiplicity (see The Factor Theorem), then:
|
A polynomial of degree n can have only an even number fewer than n real roots. |
Thus, when we count multiplicity, a cubic polynomial can have only three roots or one root; a quadratic polynomial can have only two roots or zero roots. This is useful to know when factoring a polynomial.
The Fundamental Theorem, in its most general form (involving complex numbers), has a long history. Finding the roots of polynomials is an activity that has engaged mathematicians for many centuries.