The Number e
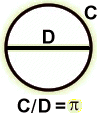Certain numbers hold celebrity status in mathematics. One such number is p , the ratio of the circumference to the diameter in any circle. Like other celebrities, p has become a part of our popular culture. In cartoons, the symbol is often used to indicate the presence of "smart" people, or even as an icon for "mathematics" itself. Indeed, many people who know very little else about mathematics are able to recite, from memory, several of the digits of p's infinite, aperiodic, decimal expansion,
p = 3.1415926536... .
Ancient and venerable, p has the aura of a very important number.
And yet, even in your most generous recollections, you've probably experienced only an occasional need to compute the circumference of a circle from its diameter, or vice versa. Why is p so important?
The answer comes from p's central place in the study of trigonometry. Trigonometry is used to model all types of repeating, periodic phenomena in nature, and the archetype of such repeating, periodic phenomena is "going around in a circle." If you haven't studied trigonometry, you may have mistaken p's cultural ubiquity for a kind of "importance," as we often do with celebrities.
You can read about the history of p here.
If you go on from trigonometry to study calculus, there is another irrational number whose role is equal in importance to that of p, though it is much less widely known in the popular culture. Among the mathematics in-crowd, however, this other celebrated constant is regarded with a special fascination. A comparative youngster to the grandfatherly p , there is a calculated mystery about it.
The number is e, with a decimal expansion that begins:
e = 2.71828182845904523536...
The number was first introduced by the mathematician John Napier, who used it in the development of his theory of logarithms in the early 1600s. His version of "natural" logarithms were abandoned almost immediately, however, in favor of "common" logarithms with a base of ten, and it was left to Leonhard Euler (1707-1783) to discover many of the number's remarkable properties. Euler was the first to use the symbol e. Despite appearances, it is unlikely that Euler named the number after himself, even though it is still sometimes referred to as "Euler's number." 1 As we will see in the first example, the number has a rightful claim to being the base for exponential functions, and so it has been suggested that Euler meant e to stand for "exponential." The truth may be even more prosaic: Euler was using the letter a in some of his other mathematical work, and e was the next vowel.
1 This term can be confusing: There is another, unrelated number usually called "Euler's constant."
In the following pages we'll investigate e's surprising appearance in several completely different contexts. You needn't understand the connection between e's appearance in all of these different settings. Use the examples, instead, to appreciate that e may have a mathematical ubiquity equal to that of p, and so, indeed, may be a number worthy of further study.
We'll begin with a careful look at e's role as the "natural" base for exponential functions and logarithms.
