| Example 2: Numerical Series | Click here to open an associated Mathcad worksheet:
|
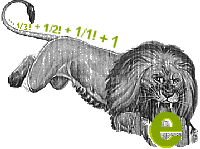You may have wondered how we come to know the digits in the infinite decimal expansion of e :
There are many formulas that are used to compute e's decimal expansion, all of them continuing on infinitely like the decimal expansion itself. For example, Euler proudly displayed the following trophies of his lion hunting 2:
These last two formulas are a little easier to understand if we write them as continued fractions:
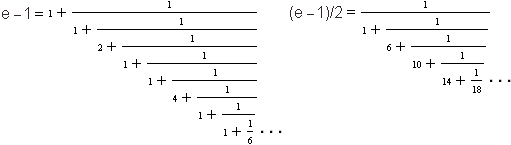
Any of these formulas can be used to give an approximation of e . We simply chop off the lion's infinite tail ... at some point 3, and then add together the numbers that remain. All of the series are convergent, in the sense that the approximations get better and better the further out we go. The formulas converge to e at quite different rates, however. Try them. Which one generates accurate values for the decimal expansion of e most quickly? Which one do you think calculators and computers use?
You will study series much more closely when you get to calculus. Series ultimately provide the clues that are used to connect e's surprising appearance in so many different contexts.
The next two examples are both set in the context of some kind of accumulation problem. In the first example, the accumulation is discrete. In the second, the accumulation is continuous. In both settings, e appears quite unexpectedly!
|
|
| Back to Contents | |