Example 5: Hyperbolic Trigonometry

Click here to open an associated Mathcad worksheet:

At its most basic level, trigonometry is nothing more than a description of "going around in a circle." The description is made using two circular functions. These functions give the  x  and the  y  coordinates of a point on the unit circle  x ² + y ² = 1  as a function of an angle  u :

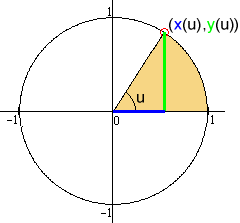
The circular coordinate functions are important enough to have special names: the cosine and the sine. We write  x(u) = cos u  and  y(u) = sin u. As  u  increases, the point  (x(u), y(u))  goes round and round, in an ideal model of many natural periodic behaviors.

Algebraically, however, there is nothing particularly special about  x ² + y ² = 1. For example, what would happen if we changed the plus to a minus? The result,  x ² – y ² = 1, is called the unit hyperbola. Its right half looks like this:

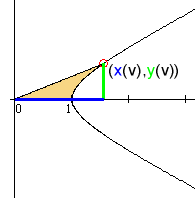
Sensibly enough, there are hyperbolic functions to give these  x  and  y  coordinates. The functions are called the hyperbolic cosine and the hyperbolic sine, respectively, and we write  x(v) = cosh v  and  y(v) = sinh v. The  v  here isn't an angle, but rather an area: Twice the shaded area in the figure above. (It turns out that the angle  u  in the definition of the circular functions can also be thought of as an area: Twice the shaded area in the top figure.) Obviously, the hyperbolic functions cannot be used to model periodic behaviors, since both  cosh v  and  sinh v  will just grow and grow as  v  increases.

Nevertheless, these functions do describe many other natural phenomena. Here, for example, is an everyday place to look for hyperbolic functions:

The curve formed by a hanging necklace is called a catenary. Its shape follows the curve of  y = cosh x.

What does this have to do with the number  e? Again, the answer is surprising: Both  sinh  and  cosh  can be written as a simple combination of exponential functions:

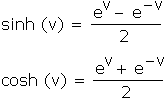
The number  e  has found yet another way to describe things "naturally."

For a final example, we'll look at still another part of mathematics: the study of permutations. Just when things seem hopelessly mixed up,  e  walks in the door to sort them out...