Just as we have various unit systems for measuring lengths (inches, feet, meters, light years, etc.), we have various unit systems for measuring angles. There are two systems in common use.
Angular Measure
Just as we have various unit systems for measuring lengths (inches, feet, meters, light years, etc.), we have various unit systems for measuring angles. There are two systems in common use.
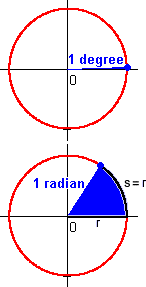
The oldest system (dating back to the Babylonians) is the degree system. In this system, a full circle is divided into 360 equal degrees. One degree, therefore, is only a very small part of a circle.
A more natural system of angle measurement – one that is based on the geometry of the circle itself – is the radian system. One radian is the angle formed when one radius is layed, like a piece of wet spaghetti, along the arc s of a circle's perimeter. Since the entire perimeter of any circle is only 2p (a bit more than six) times the radius, there are far fewer radians than degrees in a full circle.
To convert an angular measure from one system to the other, we need only remember that when a degree measure is some fraction of 360, the corresponding radian measure is the same fraction of 2p :
We can plug in for either "degrees" or "radians" and solve for the other. In this way we find, for example, that 1 radian is approximately 57.3 degrees.
The convenience of the radian system comes from the simple relationship between angle measure and arc length on the circle. By definition, one radian cuts off an arc length of one radius, two radians cuts off an arc length of two radii, and so forth. The two measures are proportional, with the radius as the constant of proportionality.
Review of proportionality: 
Thus, if r is the circle's radius, q is the angle in radians, and s is the arc length cut off by the angle, then
When the angle is measured in degrees, the relationship between s and q is still a proportional one, but the constant of proportionality is not quite so simple as r . (What would it be?)
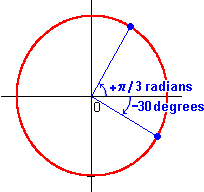
It is often convenient to give angles signs, to indicate direction. The convention is to measure positive angles in a counter-clockwise direction from some reference line (usually the x-axis), and negative angles in a clockwise direction.
