The Factor Theorem

Theorem: The number  r  is a root of a polynomial if and only if  (x – r)  is a factor.

The if and ony if tells us that the theorem goes in both directions. If  r  is a root, then  (x – r)  must be a factor. Likewise, if you can factor  (x – r)  from a polynomial, then  r  must be a root.

Both directions are useful.

One direction is obvious. If  P(x)  is a polynomial and we factor out  (x – r)  to obtain  P(x) = (x – r) Q(x) ,where  Q(x)  is the quotient polynomial, then  P(r) = (r – r) Q(r) = 0 Q(r) = 0 ; i.e.,  r  is a root. This is useful because it tells us that factoring a polynomial is equivalent to finding roots.

The other direction is less obvious, but it is easy to see its usefulness. Suppose we find – by looking at the graph, by trial and error, or by other means – a root of a polynomial. For example, suppose that we discover that  r = 5  is a root of  P(x) = x ³ – 8 x ² + 17 x – 10 . Then we know that we will be able to factor out  (x – 5)  without leaving a remainder:

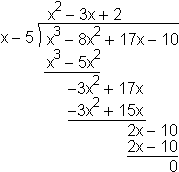
Thus  P(x) = (x – 5) (x ² – 3 x + 2) . We can now finish the job by finding any further roots of the quotient polynomial  Q(x) = x ² – 3 x + 2  using the Quadratic Formula.

The theorem guarantees a factor  (x – r)  for each root  r . It does not say that there is only one such factor for each root. In fact, it is simple to construct polynomials with arbitrary repetitions of the same factor and the same root:

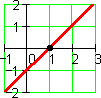
x – 1 The root has multiplicity 1.
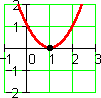
(x – 1) 2 = x 2 – x – 1 The root has multiplicity 2.
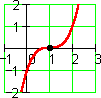
(x – 1) 3 = x 3 – 3 x 2 + 3 x – 1 The root has multiplicity 3.

Roots of multiplicity higher than  1  occur at maxima, minima, and inflection points.