Finding Sines & Cosines

To find the sine or the cosine of an arbitrary angle  q , you might imagine making a careful drawing of the unit circle with a compass, carefully adding the angle to the drawing with a protractor, and then using a ruler to carefully measure the  x  and  y  coordinates of the point where the angle intersects the circle.

The use of such mechanical methods has a long history in both geometry and trigonometry. Problems that arise when attempting to construct drawings using only a compass and a rule (a ruler without markings) led to significant historical developments in these subjects. Some of the most famous compass and rule problems, including squaring the circle, doubling the cube, and trisecting an angle, eventually led to the development of entirely new areas of mathematics.

Today, our principle mechanical tool is the computer. Computers quickly return the sines and cosines of arbitrary inputs.

Typically, computers programs like to work with inputs measured in radians rather than degrees. This is because many of the trigonometric formulas they use are much simpler when the inputs are expressed in radians. Most progams come with a "switch" that allows you to input angles in degrees, but this is just a signal to the computer that the inputs will have to be converted to radians before the program can proceed happily upon its computations.

What a program does with the inputs is another matter. It does not make measurements of a carefully constructed drawing of the unit circle and the input angle. Neither does it store huge tables of sines and cosines, covering as many angles as possible. Rather, a program will typically do something like the following:

• Remember the sines and cosines at a few simple reference angles.
  
  
• Find related sines and cosines using trigonometric identities which express natural symmetries of the circle.
  
  
• Calculate all other sines and cosines using series representations for these functions. You will learn more about series representations in calculus.

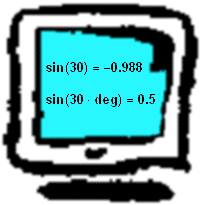
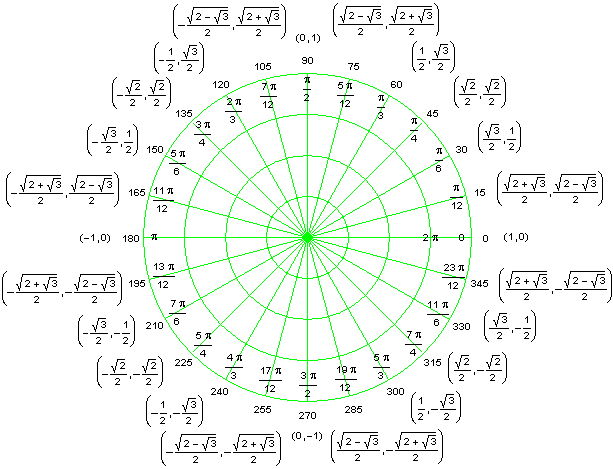
It is worth remembering the sine and the cosine at some simple reference angles, with an understanding that related angles can be found using symmetries of the circle. The following reference diagram gives some values in the first quadrant, and related values in the other quadrants. Values in the first quadrant are found using the Pythagorean Theorem. Related values are found using symmetries of the circle.