Other Trig Functions

Here are some common ratios of the sine and cosine:

• The tangent function is given by: tan(q) = sin(q) / cos(q)
  
  
• The cotangent function is given by: cot(q) = cos(q) / sin(q)
  
  
• The secant function is given by: sec(q) = 1 / cos(q)
  
  
• The cosecant function is given by: csc(q) = 1 / sin(q)

We treat these ratios like we treat rational functions: Proportional to the numerator and inversely proportional to the denominator.

Review of proportionality:

Each of these functions have roots where the numerator has roots and singularities where the denominator has roots. (See section on rational functions.) The secant and the cosecant, with a numerator that is fixed at  1 , have no roots. All of these functions have singularities.

This "rational" behavior is clear when we graph, e.g., the sine, the cosine, and the tangent together:

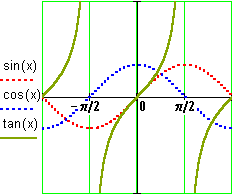
It is also clear that the tangent and the cotangent are inversely proportional to each other:

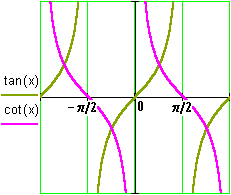
Similarly for the cosine and the secant, and the sine and the cosecant:

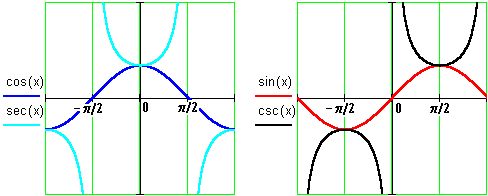
The periods of the secant and cosecant, like the cosine and the sine of which they are composed, are  2p . The tangent and the cotangent, however, repeat themselves in intervals with a length of only  p . Do you see why? (Hint:  +/- = -/+  and  +/+ = -/- .)