Proportionality

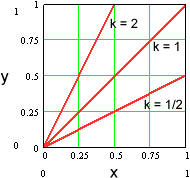
We say that two variables  x  and  y  are proportional to one another – and write  y a x – when one variable is always a constant multiple of the other. I.e., y a x  when there is some constant  k  for which  y = kx .

Notice that, in this case, doubling  x  doubles  y, tripling  x  triples  y, halving  x  halves  y, etc.

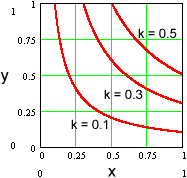
We say that two variables  x  and  y  are inversely proportional to one another when  y a 1/x . I.e., y  is inversely proportional to  x  when there is some constant  k  for which  y = k/x .

Notice that, in this case, doubling  x  halves  y, tripling  x  cuts  y  by one third, halving  x  doubles  y, etc.

In either case, we call  k  the constant of proportionality.

The relationship between proportional variables is given by a simple linear function. The constant of proportionality gives the slope.

The relationship between inversely proportional variables is given by a simple power function. The constant of proportionality gives the height of the curve.