Semi-Log Transformations of Data
Suppose a data set is actually following the trend of some hidden exponential function
If we take the logarithm of both sides of this equation (any logarithm will do) and use the laws of logarithms (see the section on algebraic representations of logarithms), we get
Now consider a new data set showing
This is linear. Linear data sets are easy to recognize.
The transformation of the data set from y vs. x to
For example, if we look again at the data set for g , together with its semi-log transformation (we use
|
|
Notice that we could not have made this transformation in the data set for h , since the output values there are negative, and we cannot take logarithms of negative numbers.
It isn't difficult to recognize the linear trend in the transformed data set, with a slope of approximately 0.04 and a y-intercept of 0.36 . (See the section on numerical representations of linear functions.) We have
This is exactly the model we found using our previous methods.
There are also graphical versions of the semi-log data transformation.
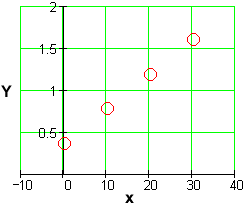
The simplest is to plot

The straight line tells us that the original data set has an exponential trend.
Alernatively, we can produce a semi-log plot of the original, untransformed data set y vs. x and look for a straight line:
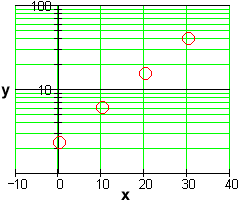
In this plot, the distances of the markings on the vertical scale above the x-axis are the logarithms of the distances used on a standard plot. The effect of the plot is to show the trends in the transformed data set without actually having to compute all of the logarithms.