Cubic Splines

Given any data set, the method of cubic splines will produce a piece-wise defined function that fits all of the data points exactly. The "pieces" are cubic polynomials, and they are found in such a way that they can be blended together smoothly, without any sudden changes of direction at the connection points.

To produce a spline, data is sorted in order of increasing  x  values. The data set is then considered in consecutive, overlapping pairs of points. Thus, if x₁ < x₂ < x₃ < ... , the data set

(x₁, y₁), (x₂, y₂), (x₃, y₃), ...

is broken down into the pairs of points {(x₁, y₁), (x₂, y₂)}, {(x₂, y₂), (x₃, y₃)}, ... etc.

Each pair of points is used to determine three cubic polynomials, known as splines. The middle polynomial must pass through both points. The left polynomial must pass through the left point and blend smoothly with the middle polynomial there. The right polynomial must pass through the right point and blend smoothly with the middle polynomial there:

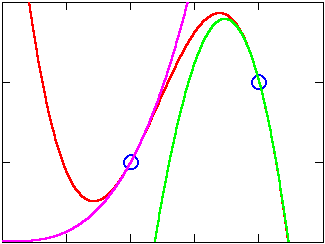
The domains (allowable inputs) of the three polynomials are then restricted to  x  values between, to the left of, and to the right of the pair of points, respectively, to produce a single piece-wise defined curve:

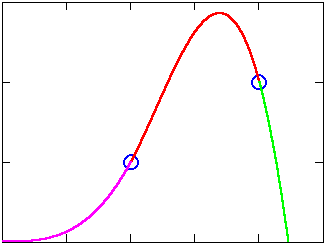
There are two things we need to be careful about if this procedure is going to smoothly connect an arbitrary collection of data points.

The first thing is that word "smoothly." What does it mean? It certainly means that consecutive splines must connect: They must share the  x  and  y  coordinates of their connecting data point. It also means that the curve must not suddenly bend and change direction at these points. This means that consecutive splines must also share the same rates of change at their connecting data point. A mathematical definition of "smoothly," and a condition on the splines that will assure smooth connections, is something that you will study in calculus.

The second thing is that the splines for each pair of data points can not be found in isolation. The right polynomial of one pair of data points must simultaneously serve as the middle polynomial of the next, overlapping pair of data points, and then as the left polynomial of the next pair, like a daisy chain, on through all of the data from left to right. Writing down conditions for the coefficients of the splines that will guarantee "connectedness" and "smoothness" leads to a great, inter-connected system of equations. Solving systems of equations is something that you would study in a course on linear algebra.

Fortunately, computers programs for producing cubic splines have been created by people who have studied both calculus and linear algebra, and they are widely available in a number of formats. One such program, which shows you how changes in the data points will affect the entire daisy chain of splines, is here.