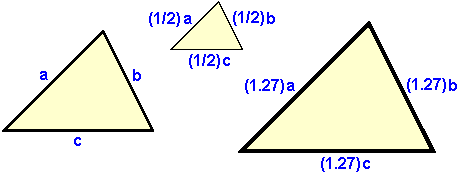
Triangle Trigonometry

Triangle trigonometry is really no different than the trigonometry of the unit circle and periodic phenomena. The key is to see the connection between triangles and what you already know about the trigonometric functions.

And this is easy. All you need to understand is geometric notion of similar triangles:

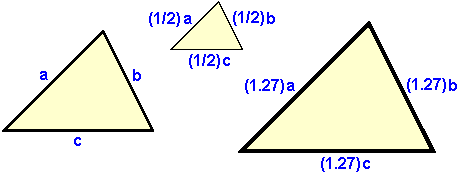
Similar triangles have the same shape but may have different sizes. Each is a dilation (a stretch or a crunch) of all other similar triangles. The dilation applies to every dimension: If one side is half as big in a similar triangle, then all sides will be half as big (or 1.27 times as big, or ...). The result is that the ratio of corresponding dimensions is the same in any two similar triangles – the dilation factor just cancels out. For example:

All right triangles (containing a  90º  angle) with a second shared angle are similar. This gives us our connection between triangle trigonometry and the trigonometric functions defined on the unit circle:

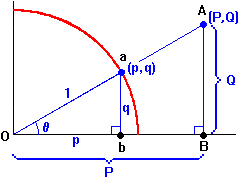
In the diagram, the right triangles  Oab  and  OAB  are similar. The smaller triangle, with  a  on the unit circle, is used to define the familiar circular functions  p = cos(q)  and  q = sin(q) . The larger triangle is of arbitrary size: It could be any right triangle containing the angle  q . The constant ratios among similar triangles then give us:

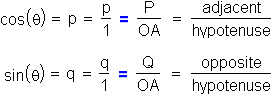
The bold, blue equalities connect the corresponding ratios in the two triangles. The terms "adjacent" and "opposite" refer to the sides of the larger triangle that are, respectively, adjacent and opposite the shared angle  q . The term "hypotenuse," as always, refers to the side opposite the right angle. The ratios above give the cosine and the sine of  q  in terms of lengths in any right triangle that includes this angle.

If you've investigated the other trig functions (previous pop-up), then you know that they are just ratios of the sine and cosine. In terms of the sides of a right triangle containing the angle  q :

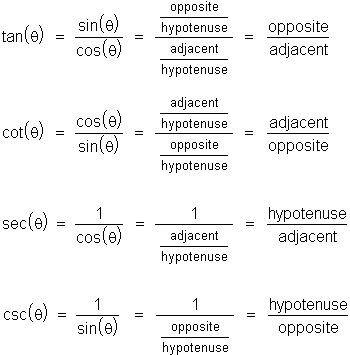
There are many useful applications of right triangle trigonometry. A few simple examples are given the following hint.

Some applications:

There is also a trigonometry of arbitrary, non-right triangles. A few useful theorems are provided in the next hint.

Theorems for non-right triangles: