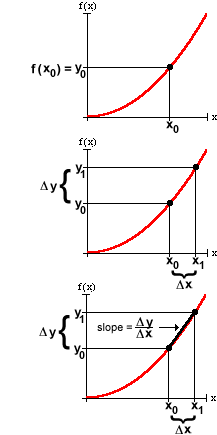
Value, Change, Rate of Change

Many important questions about functions are local questions. We often wish to know what a function's behavior is like at or near specific choices for the independent variable. For example, we may ask:

• What is the value of the function at  x = x₀?

This question asks: "For this particular value of  x, what will be the value of the associated output  y₀ = f (x₀) ?" In particular, we may wonder if this value is big or small.

• What is the change in value of the function between  x₀  and  x₁?

If  y₀ = f (x₀)  and  y₁ = f (x₁), this question asks for the change in value of the output  Dy = y₁ – y₀  as  x  changes from  x₀  to  x₁. In other words, it asks "How much has the value of the function gone up or gone down over this specific interval?"

• What is the rate of change in the value of the function between  x₀  and  x₁?

Rate, as in everyday usage, refers to "how fast." To say how fast something – like the value of a function – is changing, we need to know not only how much it has changed, but also the length of the interval over which it has changed. If  y₀ = f (x₀)  and  y₁ = f (x₁), we measure the rate of change of the function over the interval  Dx = x₁ – x₀  by:

Notice that the rate goes up if either  Dy  increases or if  Dx  decreases. That is, a certain change in value over a short interval will correspond to a greater rate of change than, say, the same change in value over a longer interval. Similarly, the rate will go down if either  Dy  decreases or if  Dx  increases.

The units for measuring rates are "change in output per change in input." Some familiar examples include miles per hour and cycles per second.