Increase, Decrease, Concavity

In 1961, after purchasing hundreds of packs of baseball cards all summer, Louisa finally unwrapped the lucky pack that contained a card for her favorite player, Orlando Cepeda. The lucky pack cost her  5  cents.

Over the years, the card accumulated in value, and in  1996  she was offered  50  dollars for the card by a collector. Louisa held on, mixing nostalgia for her childhood with the hope that the card might someday provide for her retirement.

Louisa figured the retirement value of her card as follows.

Suppose we let  t  be the number of years since  1961, and  V(t)  be the value of the card in dollars. Then we know two values of the function:  V(0) = .05  and  V(35) = 50. We can calculate the change in value  DV = 50 – .05 = 49.95  dollars, and the average rate of change in value  DV/Dt = (50 – .05)/(35 – 0) = 49.95/35, or about  1.43  dollars per year. For a retirement fifteen years after  1996, the card should be worth  50 + (1.43)(15) = 50 + 21.45 = 71.45  dollars.

But Louisa is assuming some things. First of all, she is assuming that  V(t)  will continue to be an increasing function, getting larger as time goes on. She is also assuming that the value of the card will continue to grow at exactly the same average rate as it has over the last  35  years. This need not be the case. Consider the three graphs below.

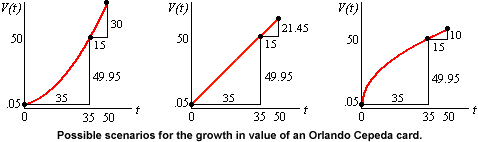
Louisa is assuming that the growth in value of her card is represented by the middle graph.

In the middle graph, the average rate of change remains constant: 50/35  is the same as  21.45/15  (both = 1.43). We say that the growth in this graph is linear.

In the first and last graphs, the average rate of change is not constant, though both of the graphs pass through the same two values as the middle graph,  V(0) = .05  and  V(35) = 50. In the first graph the average rate of change is growing:  30/15 > 49.95/35. We say that this graph is concave up. In the last graph the average rate of change is getting smaller:  10/15 < 49.95/35. We say that this graph is concave down. Obviously, the concavity of the graph will affect the retirement value of Louisa's card.

Concavity is also an important consideration when discussing the overall behavior of decreasing functions, as we will see in the examples that follow.