Example: The Utilities Problem

Click here to open an associated Mathcad worksheet:

Problem. A company decides to start a major new operation in Findlay, Ohio. They buy land for assembly plants in three separate locations around the city. Each new assembly plant requires a connection to each of Findlay's three public utilities – gas, water, and electric.

The utilities have a policy of never crossing existing connections. This assures that they will never dig up each other's lines. City codes also forbid that any lines pass through the plants themselves.

How should the three new plants be connected?

Solution. An answer to this question is not to be found by trial and error! At least, not by turning back-hoes loose in the city and hoping for the best. City engineers are more likely to build a mathematical model of the situation, and make their trials and errors there.

A mathematical model, in this case, might be nothing more than three  Xs  and three  Os  on a sheet of paper:

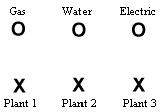
The problem is to connect the three Xs to the three Os without crossing lines.

The "mathematics" takes a very simple form here. The engineers have identified the essential features of the situation, and represented those features in a precise manner. "Mathematics" does not always mean "equations," "numbers," or "graphs."

Notice that the model does not attempt to place the plants and the utilities at their actual locations on a city map. For the mathematical problem at hand, exact placement on the page is irrelevant.

A trial solution might look something like this:

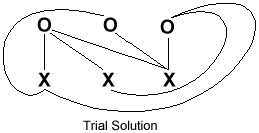
This almost works. Everything is connected, without crossed lines, except for the middle utility and the middle plant. Unfortunately, it doesn't look like there is any way to make this last connection without crossing lines or running them through a plant. No harm has been done, however – the engineer can crumple up the page and try again.

What important considerations have been left out of this model?

Back to Contents