Exercises
This second set of exercises, like the previous set of exercises, is based on the examples in the lesson. Unlike the first set of exercises, however, this set places general questions adressed in the examples in new contexts.
See if you can use what you have learned in this lesson, and your own thoughts, to provide solutions to the following. There may not always be a single correct solution, or a single way of describing that solution.
Teachers may wish to use these exercises for assignments or classroom discussion.
1. For each of the problems below, draw a simple diagram (or diagrams) that could serve as a mathematical model of the situation described. How would the model change if the particulars of the situation changed? How could the model be used to attempt to find a solution to the problem? (You do not need to actually find a solution to any of the problems described.)
- A city is located at the confluence of several rivers. Within the city, several toll bridges cross the rivers at various locations. A newspaper wishes to devise a delivery route that will start at its offices, take its drivers to all parts of the city while crossing each toll bridge no more than once, and then return to its offices.
- A state wishes to design a system of highways connecting all of its major cities. The design should make it possible to drive from any major city to any other, and it should use the least amount of roadway possible, to minimize costs.
- At a party, entering guests throw their coats into a pile. As they leave, each sleepy guest takes a coat from the pile at random. The next morning, the host wonders what the chances are that noone went home with the right coat.
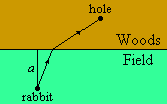
- A rabbit in a field of tall grass at the edge of a forest sees an owl circling overhead, and runs for its hole in the forest. The rabbit can run twice as fast in the forest as it can in the tall grass. What route should the rabbit take to get to its hole as quickly as possible?
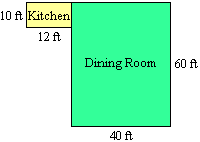
- Hayley lives on the corner of E. 88th St. and 2nd Ave. Each day she goes to visit her friend Willy, who lives at the corner of E. 63rd St. and 5th Ave. She likes to vary her route. How many different routes can she take without going out of her way?
2. For each of the problems below, give a simple formula (or formulas) that could serve as a mathematical model of the situation described. How would the model change if the particulars of the situation changed? How could the model be used to attempt to find a solution to the problem? (You do not need to actually find a solution to any of the problems described.)
- At a supermarket, the stockboy likes to create eye-catching displays by stacking up cans in tall pyramids. He wonders how many cans will be needed to make a pyramid of a certain height.
- The radius of a spiral sea-shell grows and grows as it circles its central axis. After how many turns will the shell have a diameter of 1 inch?
- A guitar amplifier sends its output back to its input, over and over, to produce feedback. After how many loops of the feedback cycle will the output overpower the amp?
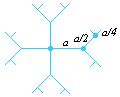
- As a snowflake grows, the number of needles multiplies as each of the needles branches. How long will it take the snowflake to grow to have 100 needles?
- Hayley likes to toss cards into a hat while she is waiting for her friend Willy to call. She usually gets about a third of her tosses into the hat. Will the hat be full before Willy calls?
3. For each of the problems below, give a simple table of values (or tables) that could serve as a mathematical model of the situation described. How would the model change if the particulars of the situation changed? How could the model be used to attempt to find a solution to the problem? (You do not need to actually find a solution to any of the problems described.)
- The Superhemotonic Mojotron, the most complicated piece of scientific equipment ever assembled, begins to shake as its dial is turned. Will the shaking break the bolts holding it to the floor?
- Each day, the water rises and falls along the posts of the dock at Penetanguishene. When is high tide?
- Each year, crop yields on the family farm vary with the weather. Will there be enough to pay for a new combine this year?
- The number of whooping cranes returning to the sanctuary each spring continued to decrease as the chemical company sold more and more fertilizer to the local farmers. Were the whooping cranes in danger of disappearing forever?
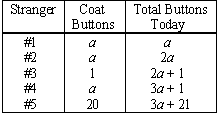
- As Hayley walks, she counts the buttons on people's coats. She "wins" when her total count equals the number on the doorway she is passing.
4. For each of the model-building exercises in 1., identify the three parts of the modeling process (formalization, mathematical deduction, and interpretation) that would be involved in "solving" the problem.
5. For each of the model-building exercises in 2., identify the three parts of the modeling process (formalization, mathematical deduction, and interpretation) that would be involved in "solving" the problem.
6. For each of the model-building exercises in 3., identify the three parts of the modeling process (formalization, mathematical deduction, and interpretation) that would be involved in "solving" the problem.
7. Each model below involves a parameter a. Explain how the value of the parameter might be determined by the "natural law" governing the situation, and say how it might vary.
- The input-output behavior of a guitar amplifier is described by the formula y = f(x) + a .
- The radius of a spiral sea shell at angle q is given by the formula r = r0 a q .
- A rabbit runs for its hole in the woods, as shown.
- A snowflake branches as shown.
- This season, Hayley notices that a-button coats are all the rage. She counts the buttons on people's coats and makes the following table in her address book.
8. Perform each of the following simple experiments. In each case, start by identifying an independent and a dependent variable. Then collect some data on the relationship between the two variables, listing your data in a table. When you feel that you have a good data set (you may wish to average several trials), plot the data on a carefully labeled graph. Finally, see if you can find a formula that could serve as a reasonable model of the relationship between the two variables. Plot the model formula together with the data.
- Poke a hole in the side of a large plastic soda bottle or coffee can. Fill the container with water and let the water leak out.
- Attach a weight to a string. Observe the period of time for one full swing (back and forth). Shorten the string and observe the new period. Repeat.
- Set out a cup of hot liquid in a room without drafts. Measure its temperature as it cools.
- Set out a cup of cold liquid in a room without drafts. Measure its temperature as it warms.
- Throw a large number of coins on the floor. Count them. Remove the coins that came up heads. Start over, using only the coins that came up tails.
9. Dawn and Herb are in the process of opening a restaurant. They plan to keep the restaurant open from 6 PM to 9 PM six days a week and offer complete dinners that range in price from $12 to $20. They are expecting about 75% occupancy for all seatings. The layout of their dinining room and kitchen is shown below. To secure financing for their venture, Dawn and Herb need to estimate their revenues for a typical week. Help them prepare their estimate, giving a clear account of your assumptions and analysis.