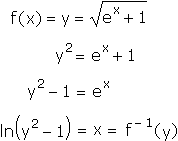
The Algebra of Inverses
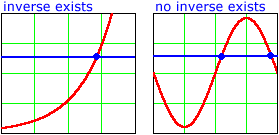
If the rule for a function f is given as a graph, then it is easy to determine if the function has an inverse, using the horizontal line test:

When a graphical rule is invertible, it is also very easy to see how to apply the inverse rule: We simply read the graph "backwards", starting with "inputs" on the y-axis and reading the "outputs" from the x-axis.
Often, however, functional rules are given to us in the form of an equation, not a graph. For example:
![]()
Such rules can, of course, be plotted, and the methods for working with graphical rules applied:
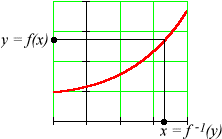
In calculus, you'll learn a general method for determining directly from an equation whether or not it is always increasing or always decreasing, and so invertible. Sometimes, however, we can make this determination with algebra alone. In the equation above, for example, f is composed of three separate functions:
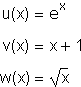
Since each one of these functions is increasing individually, the composite function
We can find an algebraic rule for the inverse of f by solving the equation