Inverse Polynomial Functions

Polynomial functions

 f(x) = a _n x ⁿ + a _{n – 1} x ^{n – 1} + ... + a ₂ x ² + a ₁ x + a ₀ 

have inverses only in special circumstances.

If the polynomial has only a single term, then it is really just a power function. It will have an inverse exactly in the cases where power functions have inverses.

If the polynomial has several terms, then it will only have an inverse if the sum of these terms is always increasing or always decreasing.

Adding together odd powers with positive coefficients (which are always increasing) is a sure bet:

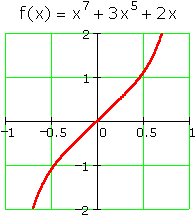
Using even powers instead won't do:

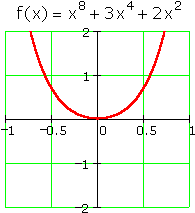
And mixing and matching even/odd powers or positive/negative coefficients typically produces wiggles:

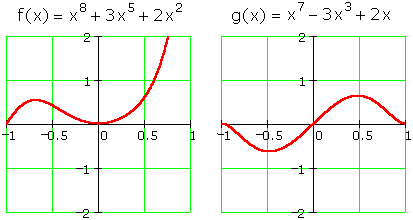
But not always:

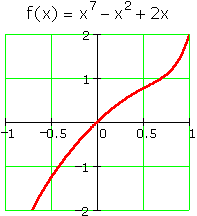
In calculus, you will learn a simple method that will quickly tell you if a given polynomial equation represents a function that is always increasing or always decreasing.

Formulas for the inverse of a polynomial, when they exist, often involve complicated combinations of roots of various degrees. For example, the simple cubic polynomial  y = f(x) = x ³ + x + 2  has the following inverse:

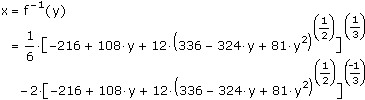
There are general, though very complicated, methods for finding the inverse formulas of cubic (degree 3) and quartic (degree 4) polynomials, when they exist. These methods solve  y = f(x)  for  x  in terms of  y  by finding the roots of  g(x) = f(x) – y  (i.e., by finding the  x  for which  g(x) = 0). You can read some of the history behind these root finding methods here.

Abel showed that the solution of the general quintic (degree 5) polynomial cannot be written as a finite formula involving only arithmetic operations and roots.