Inverse Rational Functions
Suppose
There are many ways for a rational function to fail to have an inverse.
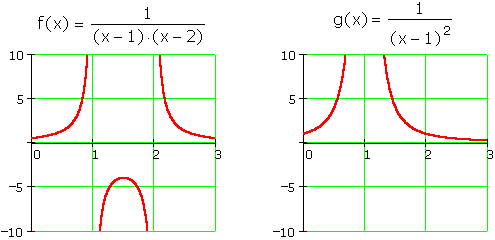
Multiple singularities, or singularities with multiplicity > 1, will not do:

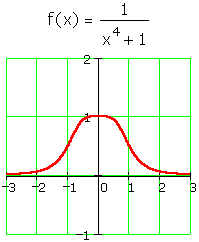
Neither will eliminating singularities altogether:
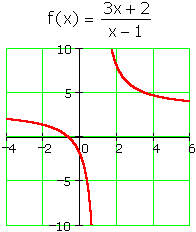
Short of a denominator of 1 (which reduces the rational function to a polynomial), the only way to arrange for an invertible rational function is to have a horizontal asymptote and just one singularity:
In this case, we solve for x in terms of y as follows:
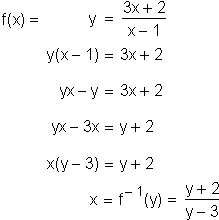
Notice that the only place where the inverse is undefined is at