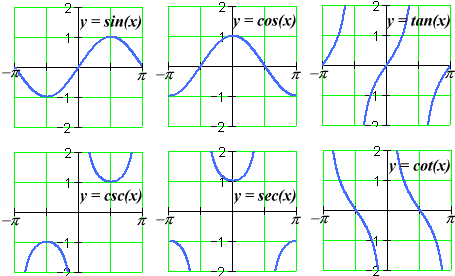
Inverse Trigonometric Functions

A quick look at the graphs of the trigonometric functions shows that absolutely none of them are invertible:

This is a consequence of the trigonometric functions' provenance in the world of periodic phenomena: output values are supposed to repeat over and over again.

Nevertheless, in calculus you will become very familiar with the usefulness of the inverse trigonometric functions: sin ^-1, cos ^-1, tan ^-1, ...etc. (Also written arcsin, arccos, arctan, ... or asin, acos, atan...)

What sort of trickery is this?!

Only this: A civilized agreement has been made among the users of trigonometric functions throughout the world. It is recognized that, because of their repetitious nature, the essential information in any trigonometric function is contained in a very small — and very invertible — part. These essential pieces are called the functions' principal branches or principal parts. They are shown in red below:

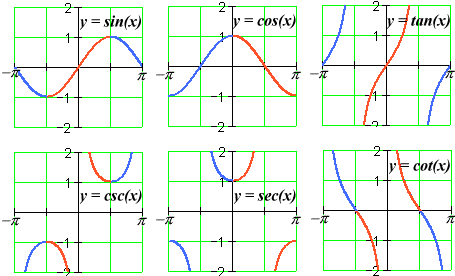
The world-wide agreement is that only the principal branches of the trigonometric functions will be considered when finding inverses. Notice that, in all cases, the principal branch is either strictly increasing or strictly decreasing (and so invertible), and the range of outputs on the branch covers the entire range of outputs for the function itself.

To see how this works, consider the sine function. If we ask the "inverse" question "Which angle has a sine of  1/2 ?", the most truthful answer is "infinitely many angles": p/6 ± 2kp  and  5p/6 ± 2kp , where  k  is any integer:

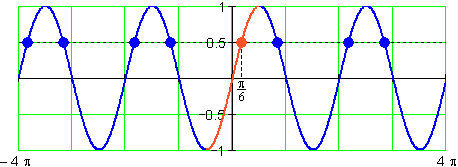
Only one of these values, however, falls on the principal branch, and so the output of  sin ^-1(1/2)  is uniquely determined: We write  sin ^-1(1/2) = p/6 .