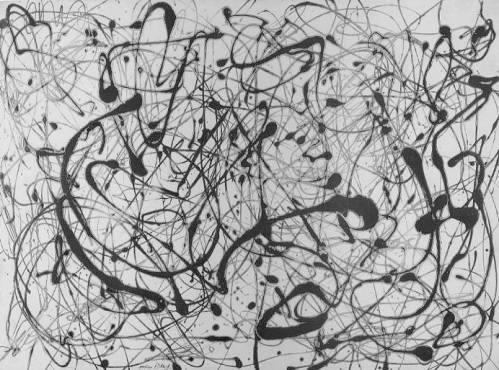Fragments of Infinity, A Kaleidoscope of Math and Art by Ivars Peterson, John Wiley & Sons, Inc

Then, unaccountably, inspiration seemed to disappear. As Pollock struggled to regain the self-confidence of those transcendent seminal encounters, his vision became murky. The lost lucidity in his work slowly translated into an acute psychological distress. He scraped and reworked the canvas that had so vexed him on that rainy night, returning to it for over half a year. Eventually, he had had enough: he picked up a 2x4, slopped blue paint along an edge, and plunged it repeatedly into the wet canvas, varying the angles in some faint residual hope of artistic gesture. It had to have felt like a desperate act, to impose something as laughable as linearity on such a tormented landscape. Nevertheless, “Blue Poles” came to be recognized as an epic exposition of human limitations—a marvelous disaster. It would sell, after Pollock’s death, for a record price of two million dollars at auction.

Mathematicians may relate to certain aspects of the story. It isn’t difficult, after all, to draw parallels between the working artist and the working mathematician. Both endeavor to express connections among abstract manifestations of the most elusive of universal concepts. Both are dependent upon specialized formal languages, incomprehensible to the great mass of the uninitiated, the insufficiently devoted, or the simply unable. Both struggle with the finite forms and structures with which we are all destined to formulate our limited visions of the infinite and the ineffable. Both, finally, must defer to creative mechanisms beyond their complete control: intuition, aesthetic judgments, and the subjective regard of their peers.

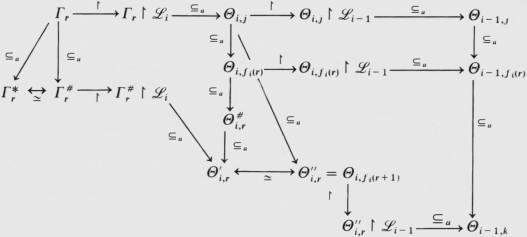
Figure 3.13, 1983, from Degrees of Unsolvability, by Manuel Lerman [3, p. 291].

It is, of course, also very easy to oversimplify these connections, leaving only a filamentary network of clichés. Not all artists are troubled alcoholics like Pollock, struggling to release something trapped within. Similarly, not all mathematicians are brilliant schizophrenics like John Nash, recognized for their idiosyncrasies as much as for their work. A persistent cultural fascination with the ultimately facile category of “genius”, combined with a sentimentality that reflexively equates intellectuals with loveless loners, only perpetuates these popular myths. Recent Hollywood treatments of both Pollock and Nash [1], [2], for example, showcase troubled individuals engaged in solitary acts of revolutionary creation. The craft, dedication, society, and often quite impersonal inspirations that form the day-to-day life of most working artists and mathematicians are not the stuff of media stardom.

Ivars Peterson, a writer of popular columns on mathematics for both the MAA and Science News, has written a book that, by way of contrast with the Hollywood blockbusters, plainly presents a selection of contemporary work-a-day artists and mathematicians who look to each other for inspiration. Each of the ten chapters in Fragments of Infinity is organized around a shared mathematical theme, explored by a particular subculture at the math/art intersection. The themes are well-trodden in the popular mathematical literature—fractals, tilings, minimal surfaces, etc.—but Peterson distinctively finds artists who use these mathematical ideas as organizing elements and mathematicians who are inspired by their conceptions. In many cases, the math/art divide is convincingly rendered superfluous, both for the individuals portrayed and for the work that they produce. It is an engaging premise. Peterson is a winning writer, and he tells these stories of collaboration and cross-fertilization with an easy-to-read simplicity.

The book, however, contains very little in the way of actual mathematics. Mathematical notation is avoided completely, and there is no sign of computer code, despite many examples of artists working with computer-assisted designs. The author seems to assume that readers will come to the book with only the most rudimentary technical knowledge. Elementary terms such as “coordinate” and “plane” are patiently described, and the reader is taken deliberately through constructions like the “unusual” Möbius strip. Higher-level mathematical ideas, when they are approached, are handled poetically, in a style that is clearly directed at a “general” audience. There is nothing wrong with writing at this level, of course. One wonders, however, who this “general” audience might be, and why they would be reading this book. Mathematicians, certainly, will look through these pages and wonder if their subject is being faithfully represented.

Artists will undoubtedly have similar reservations. The book has been published with high production values, and it includes many fine photographs of artists’ work. There is scant mention, however, of artistic materials and processes. There is nothing in the text that can really be called art criticism, either. In a typical chapter, standard artistic terms such as “conceptual” are explained, followed by anecdotes of artists who neatly fit the bill. Rather than providing satisfying analyses of artists’ interactions with their work, or with other artists, the text offers only a collection of short, tidy images. The sculptor Helaman Ferguson, for example, is described this way: “amid the roar and the dust, artist and stone engage in intimate conversation—one that can readily break into song” (p.12). The implied connection between the vibrations of the stone and the geometry of the emerging form has a mathematical resonance that seems far too convenient. Peterson often works in metaphors like this, at times saying more about his own search for expression than he does about the artist or their work. The liberties can become aggravating, as when Pollock’s paintings are flatly misrepresented as “fractal splashes” (p.2).

Peterson begins his book by saying that it is “about creativity and imagination at the intersection of mathematics and art” (p.v). He says that he will “highlight the processes of creativity, invention, and discovery intrinsic to mathematical research and to artistic endeavor” (p.vi). It is an ambitious declaration, and it sets expectations high. Indeed, throughout the book there is the recurrent suggestion that a grand connection between the two subjects will be revealed. The surface similarities between mathematicians and artists, already noted, cannot serve. What Fragments of Infinity seems to promise, tantalizingly if never quite explicitly, is some exposition of the nature of these similarities. The promise is never truly delivered.

Part of the difficulty is that the author has limited himself—unnecessarily—to representative examples of a predetermined theme. Sources come entirely from the visual arts, are disproportionately sculptural, and lean heavily on the immediate appeal of geometric forms. In an opening tour of the National Gallery in Washington D.C., for example, the author stops at the entryway to admire the elegant curves of Henry Moore’s Knife Edge Mirror Two Piece, claiming for Moore a “fascination with holes and topological transformations of space” (p.2). The author assiduously avoids walking around the building to confront Frank Stella’s Prinz Friedrich von Homburg, Ein Schauspiel, 3X, the mathematical lessons of which would be far more difficult to encapsulate. (It is possible that the author’s visit predated installation of Stella’s work, but one might pick from any number of similarly perplexing pieces in and around the gallery.) Given such limited observations, it seems doubtful, right from the start, that the author will be able to generalize his conclusions convincingly to all of art and mathematics, however suggestively they may be presented.

Peterson has put himself face-to-face with the fundamental impediment to popular writing: To write an account of a difficult subject, it becomes necessary to accommodate the lay reader by leaving out most of the difficult things. When these difficulties are an essential, even a defining, characteristic of the subject, a thorny representational dilemma presents itself. The problem, of course, is only compounded when two difficult subjects are treated simultaneously. Art and mathematics both challenge us to express difficult things—concretely, exactly, and in a language that is appropriate to the task. Peterson has made a commendable effort to hurdle over this impediment with stories, metaphors, and poetics, but the missing complexities—the mortar that holds these subjects together— finally make Fragments of Infinity impossible to assemble.

There is another difficulty inherent in Peterson’s approach, a deeper one. It arises from the casual application of an unexamined system of equations relating the structures and forms of mathematics with those of the artist. In simplest form, the presence of structure in an artwork, in itself, is equated with mathematical intent. Peterson ably demonstrates that mathematical structures can lead artists to a certain kind of compositional discipline. Strict mathematical discipline, however, is antithetical to many of the most fundamental tenets that have informed modern art. The Soviet painter and designer El Lissitzky was very explicit about this: “The parallels between Art and mathematics must be drawn very carefully, for every time they overlap, it is fatal for Art.” [4, p.348] Later, in another context (but just as typically), the American painter Robert Motherwell wrote that “...modern painting ...is symbolic and poetic, not discursive and descriptive. …the latter is always trying to infiltrate modern painting, usually under the tag of some ‘humanism’ or another. What shit!”[5, p.155]

There is a long history of popular accounts that link contemporary art to contemporary ideas in math and science. From parlor primers to magazine articles to coffee table books, they have usually been written in the service of some sort of democratic “popularization”, and the associations that they make have almost always been exaggerated. Lissitzky, for example, has been persistently aligned with explorations in multi-dimensional geometry made by his mathematical contemporaries. Lissitzky’s socialist perspective, and his deep involvement with the history of graphic design—both probably more influential in his art—only confuse easy-to-digest stories of his mathematical vision. An example in recent years is the spate of books, posters, and T-shirts extolling the wonders of “fractal art”, which marketably replace the subtleties of art history with the inexpressive complexities of form.

The truth is that when artists order their work, their notions of harmony, unity, and precision often come from sources that are anything but mathematical. Take, for example, an artist that Peterson features in Fragments of Infinity. Arlene Stamp was a high school mathematics teacher before turning to art full-time. She won a commission to create a mosaic for Toronto’s Downsview subway station by suggesting a non-repeating pattern “based” on the digits of pi. The conception of the design proceeded along the following lines. First, an initial state of the mosaic was imagined, consisting of a sequence of rectangular units, side by side, each ten tiles wide. In the next stage, Stamp imagined each rectangular unit shifted over the previous unit by a number of tiles rigorously determined by the sequence of digits in pi’s decimal expansion. Finally, the amount of overlap occurring along any column in the design was to be translated into a particular color of tile. This would all seem very algorithmic, if Stamp had followed the instruction set—but she didn’t. During the construction, she found it necessary to incorporate a variety of inexact human gestures to express her ideas. Peterson tells us that “some regions of overlap may end up as many as three or four layers thick” (p.92). Stamp, however, “used four sets of eight colors for the project, deploying them in different ways on surfaces in various parts of the station” (p.92). When the final mosaic is considered, we must give Stamp her due credit as an artist. Only then can we appreciate the many choices that she has made—to arrange the tiles, to shift the tiles, to count the overlaps, to choose the colors in various places—that have no basis in mathematics. The mosaic, in the end, is not strictly about pi. Stamp herself says: “I am interested in the beauty of embedded possibility”(p.94).

Many other artists could serve as examples of the kinds of mistaken impressions that can arise from a too-easy calculus of form and mathematics. Ellsworth Kelly, a contemporary painter, would seem to fit nicely among the artists in Peterson’s book. Kelly’s paintings are simple and geometric, composed of curving fields of primary color, expressing their exuberance through the exquisite tensions of tangency between various curves in the paintings and between the curves and the edges of the canvas. The carefully poised kisses between Kelly’s forms give the viewer the same kind of “Oh!” that a mathematician might experience when discovering a uniqueness theorem. Kelly’s great gift is his ability to see these forms, in all of their everyday manifestations. He has painted plants, shadows, reflections, bridge arches, and hills, all in the same hard-edged geometric distillations. The colors with which he floods his geometry express the sheer joy of seeing. If Kelly is “mathematical”, he has invented the term for himself. His abstractions from the natural world are something that we respond to intuitively, in a way that a purely mathematical art could never achieve.

Jasper Johns, another contemporary painter, offers further illustration. Johns has painted the numbers from one to nine, and has composed many other paintings around various organizations of these digits. Is Johns interested in number theory? It’s doubtful. What the numbers represent, in Johns’ language, is form itself, made visible through familiar, everyday exemplars. The forms that Johns chooses are often iconic, suggesting larger constraints in our everyday life. He is famous, for example, for having painted the American flag. Johns’ paintings struggle with these forms, working with thick layers of paint, in a discourse that is inward and painterly as much as it is outward and political. To focus on the underlining lines, rectangles, and forms of Johns’ Flag—to call them “mathematical”—would reduce the painting, quite inaccurately, to the clean lines and assured colors of a “United We Stand” bumper sticker.

Perhaps, however, the difficulty of drawing too close a correspondence between art and mathematics is best illustrated by considering the set difference—the artists and mathematicians who would not sit comfortably in any grand commonality, however much they may appreciate the work that is accomplished in the opposing sphere. Among mathematicians, this might include a large group of applied practitioners, many formalists (though I certainly know logicians who revel in the visual beauty of their symbolism), and certain Platonists, inspired by forms that they perceive to be super-human, beyond the lesser, personal impulses of art.

Among artists, the avant-garde pioneer Robert Wilson comes to mind. Known for his epic theatrical productions, especially for the stage designs of his many operas, Wilson has also found expression through drawing, painting, and sculpture. A recent installation piece, 14 Stations, combines all of these influences. Wilson says of it [9, p.3]:

My work is an environment, an installation that brings together elements of architecture, sculpture, art, music, and language. In a certain sense, it is a mental landscape. Call it an encounter of different cultural traditions, in which I have tried to invent my own language. …I always work with a horizontal line, which stands for time, and a vertical line, which, for me, always means space. This is something personal…

The vertical line, in this case, is a boardwalk that takes viewer past a series of fourteen small cottages, arrayed to either side. The interior of each cottage is examined through a small window, admitting only a single viewer at a time. What one sees, hears, and smells, in each case, is a carefully choreographed tableau—completely outside of one’s waking experience—that immediately strikes at the gut. The cumulative effect, as one wanders the entire installation, is undeniably affecting, though it is difficult to make much “sense” of the reaction. Wilson’s relation to the formal order of the piece, much of it appropriated from religious tradition, is ambiguous and unsettling. Taking Johns one step further, Wilson uses the formalism to question, and perhaps even repudiate, its very idea. Robert Wilson is not a mathematician.

Artists are constantly struggling with the limits imposed by their media. Painters like Pollock, Kelly, and Johns alternately fight, then celebrate, the restrictions of their flat, framed arena. Musicians—like Coleman Hawkins—struggle within traditions of composition and performance that, at the same time, carry with them the rich formal history of their music. Writers, from Pushkin to Pynchon, re-invent literature, but do so on a stage that has been set by generations. Mathematicians, also, must work within their subject’s history and limitations. Every mathematician has experienced a surprising counterexample, seen a conjecture disproved, and had to reconsider the outlines of the dimly lit subchamber of mathematics they call their own. Turing and Gödel, and the complexity theorists who have followed, have made fundamental limitative theorems a fact of mathematical life. Still, like artists, mathematicians regroup, consider their progress, and move on, exploring new directions and new possibilities.

Artists remind us of another limit—our own. Whatever medium is chosen, and whatever forms are imposed, expressions of our collective human understanding never feel finally, satisfyingly, complete. Pynchon writes metaphorically of Mason and Dixon and their army of axe-wielding Colonials plowing through the mysteries of the American wilderness at precisely 39^o 43' N. [7] Like Pollock’s blue poles, the meager structures that we force upon a world that is so vastly different from ourselves may seem laughable. It would seem that way, at least, if those structures weren’t such a fundamental part of who we are.

Peterson quotes the geometer H.S.M. Coxeter, saying of visualizations in chaos theory that “It makes it almost embarrassing for abstract artists to do abstract art because these are things that are so varied and so beautiful that one doesn’t need to go any further” (p.133). This is chutzpah, on a cosmological scale. There is always further—infinitely further. Artists and mathematicians know this in their bones. Together they survey the universe, extending away from them in myriad dimensions, and from within the tiny perimeter that they are able to carve out, they express what they can see, and what others may see. It is this shared sense of place and purpose, perhaps, that connects artists and mathematicians most fundamentally.

REFERENCES

1. E. Harris (dir.), Pollock, Sony Pictures, Culver City, CA, 2000.

2. R. Howard (dir.), A Beautiful Mind, Universal Studios, Universal City, CA, 2001.

3. M. Lerman, Degrees of Unsolvability, Springer-Verlag, New York, NY, 1983.

4. E. Lissitzky, Art and pangeometry, in E. Lissitzky, S. Küppers (eds.),
El Lissitzky: Life, Letters, Texts, New York Graphic Society, Greenwich, CT, 1925/1968, 348-354.

5. R. Motherwell, Letter to Frank O’Hara, in S. Terenzio (ed.),
The Collected Writings of Robert Motherwell, University of California Press, Berkeley, CA, 1992, 147-155.

6. S. Naifeh, G. White Smith, Jackson Pollock, HarperCollins, New York, NY, 1989.

7. T. Pynchon, Mason & Dixon, Henry Holt and Company, New York, NY, 1997.

8. K. Varnedoe, P. Karmel (eds.), Jackson Pollock, The Museum of Modern Art, New York, NY, 1998.

9. R. Wilson, 14 Stations, installation guide, Massachusetts Museum of Contemporary Art, North Adams, MA, 2002.

The MathWorks, 3 Apple Hill Dr., Natick, MA 01760

wmueller@alum.mit.edu
http://www.wmueller.com

Number 14, 1948, by Jackson Pollock [8, p.239].