 When we wrote:
When we wrote:
The Algebra of Complex Numbers
 When we wrote:
When we wrote:
![]()
we were making some assumptions about the new, "complex" system in which real and imaginary numbers co-mingle as if they were old friends. Certain operations — factoring out the
In fact, adding the imaginary numbers with their "unusual" negative squares can be accomodated into an integrated system that does not present any further surprises. In the complex number system, real numbers continue about their business as usual. We "imagine" only new roots.
This is good news: When working with complex numbers, we will not have to sweep away all of the algebra and arithmetic we have learned in an effort to please our new "guests".
Here's how the mutual accomodation works.
First, we will have to acknowledge the presence of the imaginary number i , with its exotic personal habits:
![]()
After that, nothing else needs to be said. Real numbers behave as before. "Complex" numbers combine the two world-views only when necessary. Here are some examples:
![]()
![]()
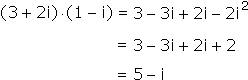
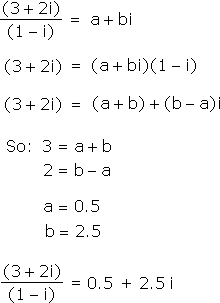
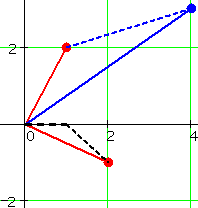
![]() Explore the geometry of complex arithmetic
Explore the geometry of complex arithmetic
|
|
|
|
| Back to Contents | ||