All complex numbers  z = a + bi  are a "complex" of just two parts:

The real part: Re(z) = a

The imaginary part: Im(z) = b

When  Re(z) = 0  we say that  z  is  pure imaginary; when  Im(z) = 0  we say that  z  is  pure real.

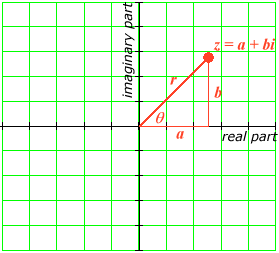
Both  Re(z)  and  Im(z)  are real numbers. Thus, any complex number can be pictured as an ordered pair of real numbers,  (a, b) . We know all about ordered pairs of real numbers. To visualize them, we plot them in a plane:

This picture of the complex plane (often called an Argand diagram, though the idea is generally attributed to Wessel) allows us to assign some familiar attributes to complex numbers.

For example, we assign a "size" to real numbers  x  by giving the absolute value  |x| . This tells us how far  x  is from the origin, regardless of its direction. We can likewise measure the distance  r  of a complex number  z  from the origin, by using the Cartesian distance formula:

This "size" of a complex number is often called its modulus.

Similarly, every real number has a "direction" assigned to it: either  +  or  – , depending on whether we head right or left from the origin, respectively. The picture above shows that the situation is not quite so simple for complex numbers. Complex numbers may extend away from the origin in any clock-face direction. To specify a direction, we give the angle  q , measured counter-clockwise up from the x-axis to the line segment containing the origin and the complex number. Note that:

This "direction" of a complex number is often called its argument.

The difference between describing a complex number with the pair  (a, b)  and the pair  (r, q)  is the difference between using Cartesian coordinates and polar coordinates, respectively.

  Review of polar coordinates

The following example shows how polar coordinates  (r, q)  like those used to describe complex numbers can also be used to give simplified descriptions of curves with certain "polar" symmetry:

  Explore polar curves

The two displayed formulas above, for the modulus  r  and the argument  q  in terms of  a  and  b , provide a kind of "translation" between the two systems of representation.