Transient & Long-Term Behaviors

When observing a sequence of outputs in application, we frequently ignore transient fluctuations in the values with a view towards long-term behavior.

For example, the value of an investment may vary widely before finding its true market value. A machine may go through temporary gyrations when it is first turned on. A prodigal son, to his mother's delight, may eventually settle down.

If we are describing a sequence in mathematical terms, transient behaviors are those that occur for only some initial, finite number of inputs. Long-term behaviors are those that occur eventually, for all large inputs.

• A property of the sequence  {a_n}  is transient if there is an input  N  after which  (n > N)  the property disappears.
  
  
• A property of the sequence  {a_n}  is long-term if there is an input  N  after which  (n > N)  the property is always present.

As an example, consider the sequence with the general term  a_n = 10^–(.005)n . The first few terms (with inputs from the positive integers) look approximately like this:

0.989, 0.977, 0.966, 0.955, 0.944, ...

These terms all have the property that  a_n > 0.9 . This property is clearly transient, however, since the values are outputs from a decaying exponential function. In fact,  a₉ = 0.902 ,  a₁₀ = 0.891 , and  a_n < 0.9  for all  n > 9 .

This same sequence has the long-term property that  a_n < 0.1 . It is clear, by the decreasing nature of the genral term, that once the terms of the sequence have this property they will not lose it:

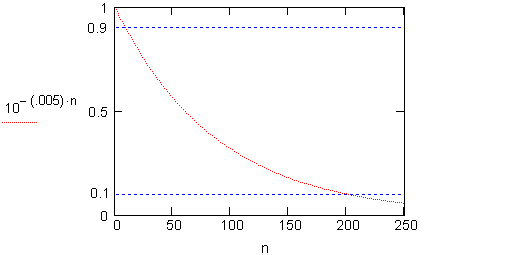
It isn't difficult to see when the sequence drops forever below  0.1 :

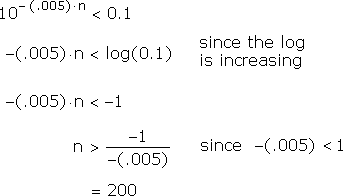
Thus, this sequence has the property that  a_n < 0.1  for all  n > 200 .

In fact, this sequence has the long-term property that  a_n < e  for any  e > 0 . Depending on the size of  e , it may take more or less terms until this becomes a permanent property of the sequence, but we can always, eventually, make the terms in the sequence as small as we like. In a case such as this, we say that the sequence converges to  0 .