Convergence & Divergence

The sequence  a_n = 10^–(.005)n  converges to  0  because the distance between any term in the sequence and  0  is eventually as small as we wish (i.e., less than any  e > 0). This is generally what we mean when we use the word "converge" to describe a sequence that eventually "settles down" to a particular value:

Definition: A sequence  {a_n}  converges to the value  a  if for any  e > 0  there is an input  N  such that  | a_n – a | < e  whenever  n > N .

When a sequence fails to converge we say that it diverges.

Consider another example:  a_n = 3 + (1/n)sin(n) . A plot of the first  50  terms looks like this:

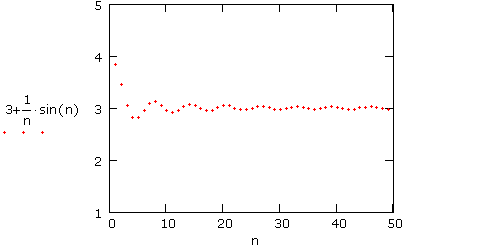
Although the terms gyrate up and down, they do seem to be "settling down" to a value of  3 . Does the sequence actually converge to  3 ?

To say so conclusively, we would have to be able show that, in the long-term, | a_n – 3 | < e  for any  e > 0 . Precisely, we would have to exhibit the  N  (dependent on  e , of course) so that  | a_n – 3 | < e  when  n > N .

This isn't difficult:

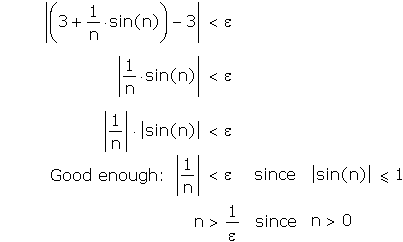
So: Every term in the sequence is within  1/10  of  3  once  n > 10 , within  1/100  of  3  once  n > 100 , etc. The sequence of values "settles down" to  3 , and we can even say after which point all further terms will be within a given distance.

Divergent sequences are just as common as convergent ones. Sequences diverge either because they are "all over the place", or else because they increase or decrease without limit:

  Explore sequences