To expand our thinking from scalar quantities to the quantities described by vectors and matricies, we must also expand our notion of function.

The general idea is always the same: A function is a rule which describes how to uniquely determine an output from an input. However, we must consider what it means for a function to have inputs and outputs that are vectors or matricies.

We've noted that functions of the form  y = f(x)  are called scalar functions (outputs) of a scalar variable (inputs). We've become very familiar with these functions in our study of precalculus.

What about:

• Vector functions of a scalar variable: e.g. (x(t), y(t)) = f(t) ?
  
  
• Scalar functions of a vector variable: e.g. z = f(x, y) ?
  
  
• Vector functions of a vector variable: e.g. (x(s, t), y(s, t)) = f(s, t) ?
  
  
• Any of the above combinations, with "matrix" replacing "vector" or "scalar"?
  
  

Obviously, there are a lot of possibilities. All of the possibilities occur frequently in applications.

Vector functions of a scalar variable are often called parametric curves. The tip of the vector  (x(t), y(t))  traces out a path as the input  t  varys. The individual coordinate functions  x(t)  and  y(t)  are just scalar functions of a scalar variable. Parametric curves model many types of motion, with the vector output specifying position and the scalar input representing time.   Explore parametric equations   Explore parametric curves
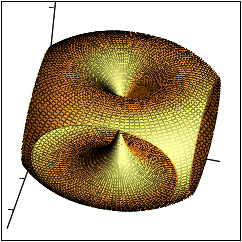
Scalar functions of a vector variable are studied in advanced calculus. Their plots are surfaces rather than curves. To picture these functions, we need to move beyond the 2D x-y plots with which we have become familiar in precalculus. Functions of the form  z = f(x, y)  can be plotted in 3D using the xy-plane for inputs and a perpendicular z-axis for outputs. If there are more than two inputs determining the output these surfaces become "higher dimensional", and we must imagine them in new ways.   Explore 3D surfaces   Explore higher dimensional surfaces
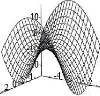
Vector functions of a vector variable were mentioned earlier in the discussion of river currents. These vector fields assign a vector – a number and a direction – to every point in the xy-plane or in xyz-space. Vector fields model phenomena as diverse as atmospheric currents, complex motions of the economy, and electromagnetic fields.   Explore vector fields