If vectors and matricies aren't numbers, does it make any sense to talk about their arithmetic and algebra?

To do so, we would first have to agree on some very basic notions, such as the meaning of "adding" two vectors, "multiplying" two matricies, and so forth.

One way to do this would be "number-by-number", performing familiar operations from the real or complex numbers at corresponding locations in the vector or matrix, like this:

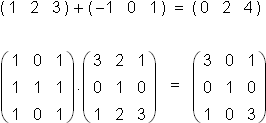
We certainly could develop an algebra for vectors and matricies this way. The question would then be: Why?

Put another way: Would such an algebra be useful? The answer to this, formulated only after a long history of attempting to use vectors and matricies in application, is limited: Such an algebra would be somewhat useful.

Indeed, operations such as the following, each of them "number-by-number", are extremely useful in application, and they have become standard definitions in vector and matrix arithmetic:

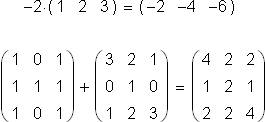
Other standards have evolved, however, for other operations:

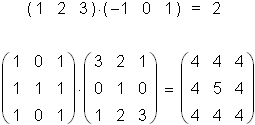
Useful definitions for the operations of vector and matrix arithmetic, and a study of the algebra that results, are usually taken up in a course in linear algebra. Linear algebra, when studied in context, neither preceeds nor follows the study of calculus. It is properly placed beside the study of calculus.

You will see vectors and matricies in many parts of calculus, and some acquaintance with their algebra will be assumed.

If you would like a little preview...

• You can read about the basics of vector arithmetic here, and then do some experimenting here and here.
  
  
• You can read about the basics of matrix arithmetic here, and then do some experimenting here.

  Explore Mathcad's linear algebra functions