Linear Functions

Algebraic Representation

f(x) = a + bx

Algebraically, linear functions are a two parameter family. The parameter  a  is called the function's y-intercept and the parameter  b  is called the slope. Together, they completely determine a linear function's input-output behavior.

Notice that  f(0) = a : The y-intercept is the output when the input is  0.

When  a = 0  the function simplifies to  y = f(x) = bx, or a proportional relationship between  y  and  x  with  b  as the constant of proportionality.

Review of proportionality:

If  (x₀, y₀)  and  (x₁, y₁)  are any two input-output pairs for the function, then

That is, the slope gives the average rate of change between any two points. Since this rate is the same regardless of the input-output pairs chosen, we see that linear functions have a constant rate of change.

Larger values of  b  mean larger rates of change for the function; smaller values mean smaller rates. Positive values of  b  give positive rates of change, or increasing functions; negative values give decreasing functions.

When  b = 0  the function simplifies to  y = f(x) = a, or a constant function with the same output for every input.

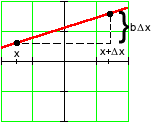
The key algebraic property of linear functions is the following: That is, increasing any input  x  by a constant interval  Dx  changes the output by a constant interval  bDx . Said another way, if the input changes by  Dx , then the output changes by the slope times  Dx . This is the property of linear functions that is most easy to recognize in modeling situations.