Exponential Functions

Modeling Representation

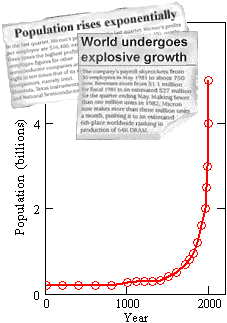Exponential functions have made their way into the popular vernacular. Often, news reports will marvel at the exponential growth of something or other: Populations, stock prices, grocery bills, etc. When referring to growth rates, the word exponential has become synonymous with explosive.

Exponential functions can indeed grow at startling rates. When their graphs are viewed over specific input-output ranges, they can seem to turn quickly from a plodding increase to a steep vertical rise.

Still, not every steep vertical rise is modeled by an exponential function. Early data on the spread of the HIV virus was modeled much more closely by a steeply rising power function than it was by an exponential function. Island populations that grow steeply at first but level off once the island has reached its capacity may be better modeled by a logistic function. When functions rise so steeply that they become arbitrarily large in a fixed interval – like the force between colliding electrons – rational functions may be the modeling family to call on.

All quickly growing functions share the characteristic that the bigger they get, the faster they grow. What distinguishes true exponential growth is a simple, and widely encountered, form of increase. In exponential growth, the output value is actually proportional to the growth rate (i.e., they are just multiples of one another).

Review of proportionality:

Exponential functions can also decrease, though these members of the family make the news less often. Their behavior, however, is the same: The rate (in this case, a negative rate) of decrease is proportional to the value of the function. Said another way, the smaller these functions get, the more slowly they decrease.

Exponential functions model rates of increase or decrease that are proportional to the value of the function.

Small value, proportionally small rate of change. Big value, proportionally big rate of change.

Exponential functions are often found in situations that involve proportional accumulation in a geometric sequence.

Review of arithmetic and geometric sequences:

Here are some other places to look for exponential growth and decay:

The growth of resource-rich populations. (kudzu vines vs. time)

Savings accumulating compound interest. (amount vs. time)

The spread of rumours. (insiders vs. time)

The rise and fall of fashions. (hats vs. time)

A cooling beverage. (temperature vs. time)

Atmospheric pressure at rising altitudes. (pressure vs. height)