Exponential Functions

Algebraic Representation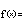

f(x) = a b x

All exponential functions are relatives of this primitive, two parameter family. Variations within the extended family are merley shifts, stretches, and transformations of this common stock.

The parameter  a  is called the function's y-intercept and the parameter  b  is called the base. Together, they completely determine an exponential function's input-output behavior.

Notice that  f(0) = ab⁰ = a1 = a : The y-intercept is the output when the input is  0.

When  a = 0  or  b = 0  the function simplifies to  y = f(x) = 0 , or a trivial constant function whose output is  0  for every input. When  b = 1  the function simplifies to  y = f(x) = a1^x = a1 = a , or a constant function whose output is  a  for every input.

Since many expressions with negative bases – like  (–1)^1/2  or  (–5.3)^7/4 – make no algebraic sense (they do not define any real number), and since a base of  0  leads to a trivial constant function, we usually add the following restriction to exponential functions:

The base  b  in an exponential function must be positive.

Because we only work with positive bases,  b^x  is always positive. The values of  f(x) , therefore, are either always positive or always negative, depending on the sign of  a . Exponential functions live entirely on one side or the other of the x-axis. We say that they have a limited range.

The base  b  determines the rate of growth or decay:

• If  0 < b < 1 , the function decays as  x  increases. (E.g., (1/2)¹ > (1/2)² > (1/2)³.) Smaller values of  b  lead to faster rates of decay.
  
  
• If  b > 1 , the function grows as  x  increases. (E.g., (2)¹ < (2)² < (2)³.) Larger values of  b  lead to faster rates of growth.
  
  

The key algebraic property of exponential functions is the following:

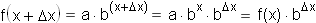
That is, increasing any input  x  by a constant interval  Dx  changes the output by a constant multiple  b^Dx . This is the property of exponential functions that is most easy to recognize in modeling situations.

There are a few important special cases of the above property:

• When  b > 1  (growth), we may choose  Dx  so that  b^Dx = 2 . Then for every  x ,  f(x + Dx) = 2f(x) . We call this input interval  Dx  the doubling time of the function. Every growing exponential has a unique doubling time.
  
  
• When  0 < b < 1  (decay), we may choose  Dx  so that  b^Dx = 1/e , where  e = 2.71828... . Then for every  x ,  f(x + Dx) = f(x)/e . We call this input interval  Dx  the critical time of the function. Every decaying exponential has a unique critical time.
  
  

You may be wondering about the number  e = 2.71828...  that is used to determine the critical time of a decaying exponential. What is this number? It is sometimes called the natural exponential base, and you will find out much more about it when you study calculus. If you're curious now, you can learn more about the number  e  by exploring some of the examples in the following pop-up:

The Number e:

The word "natural" in "natural exponential base" suggests a certain importance. Indeed, in calculus and in many applications, b = e  is the base of choice for exponential functions. This can always be arranged, since for any  b > 0  we can find a  k  so that e^k = b . We can then re-write f(x) = ab^x  as:

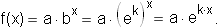
That is, any exponential function can be re-written with the natural base, provided we multiply the exponent by an appropriate factor  k . This conversion factor is called the natural logarithm of  b, and we write  k = log_e b , or simply  k = ln (b) .