Exponential Functions

Numeric Representation

x g(x) 0 2.30 10 5.97 20 15.47 30 40.13

x h(x) 0 –1.60 2 –0.88 7 –0.20 10 –0.08

To recognize an exponential trend in a data set, we make use of the key algebraic property of exponential functions  f(x) = a b ^x . Namely:

We can read this equation this way: If the input  x  is increased by a constant interval (Dx), then the output  f(x)  will increase by a constant multiple (b ^Dx).

For data sets with constant intervals between inputs, this is an easy pattern to recognize:

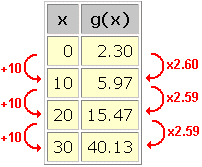
In this data set, we see an approximately exponential trend with  Dx = 10  and  b ^Dx = 2.6 . Thus, the data may be represented by an exponential function with base  b = (2.6) ^1/10 = 1.1 . The y-intercept  a  appears explicitly in the data set: 2.30 . If the y-intercept had not appeared explicitly – say the data began at  x = 10  – then we could have pluggged in any data point and solved for  a . For example,

f(10) = a (1.1) ¹⁰ = 5.97

a = 5.97 / (1.1) ¹⁰ = 2.30

We arrive at the following model for this data set:

g(x) = (2.3) (1.1) ^x

This equation can be used to interpolate or extrapolate further data values.

Be careful: Because of the rapid rates of change in exponential functions, small variations in the model base  b  can produce sizable differences in predicted values.

What if a data set has not been recorded at equal intervals of the input? We can rewrite the key algebraic property this way:

[f(x + Dx) / f(x)] ^1/Dx = b

This form of the equation can be read: Whatever the increase in input (Dx) between two data points, [f(x + Dx) / f(x)] ^1/Dx remains constant (b).

We can recognize this pattern even in data sets without constant intervals between the inputs:

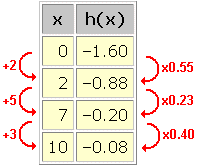
Nothing looks constant at first, but when we calculate the various [f(x + Dx) / f(x)] ^1/Dx we find:

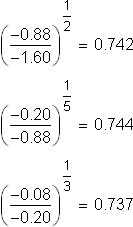
A constant base of approximately  b = 0.74  is hiding in the data. We find the y-intercept  a = –1.6  as above, and model this data with the exponential equation:

h(x) = (–1.6) (0.74) ^x

There is another method for discovering exponential trends in data sets, called a semi-log transformation. To find out more, read the hint below.

Semi-log transformations of exponential data: