Logarithmic Functions

Modeling Representation

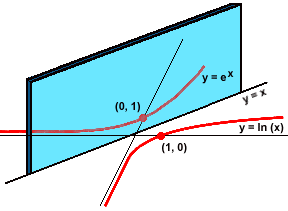
Logarithmic functions are just the inverses of exponentials. Where an exponential function may start slowly and then grow explosively, a logarithm can grow explosively and then turn a corner, making further accumulations at an excrutiatingly gradual pace.

The inverse nature of the exponential and logarithmic families carries over to every detail of their behavior.

In old Superman comic books, Superman would sometimes visit the Bizzaro World, located on a planet just like Earth, but on the opposite side of the sun. In the Bizzaro World, everything was supposed to be the exact "mirror" of what it was on Earth: People read English from right to left, Mona Lisa looked in the opposite direction, clocks ran in reverse. Reading about the Bizzaro World was disorienting, because it seemed impossible to get everything backwards. But exponentials and logarithms do.

This gives us a good way to think about situations that are modeled by logarithms. Remember: Exponential functions model rates of increase or decrease that are proportional to the value of the function. So:

Logarithms model rates of increase or decrease that are inversely proportional to the value of the function.

Review of proportionality:

Small value, proportionally big rate of change. Big value, proportionally small rate of change. The rate of change for logarithms is a multiple of the reciprocal of the value. Exactly the inverse of exponential behavior.

Here are some places to look for logarithms:

• Musical staff for notes. (distance vs. frequency)
  
  
• Richter scale for earthquakes. (magnitude vs. energy)
  
  
• Measurement of sound. (decibels vs. intensity)
  
  
  
• Star magnitudes. (magnitude vs. brightness)
  
  
• Cram studying. (amount forgotten vs. time)