Logarithmic Functions

Algebraic Representation

f(x) = a log b(x)

Like an exponential, a logarithm's essential features can be described with just two parameters.

Like an exponential, the parameter  b  is called the base.

Unlike an exponential, the parameter  a  is not the y-intercept! Indeed, members of this basic family of logarithms have no y-intercepts. To discover the meaning of  a ,  we must consider more closely the inverse nature of exponentials and logarithms.

Recall that if  e^k = b , we write  k = log_e b  (or  k = ln (b) ). We use the same notation for any base. Thus, if  b^k = c , we write  k = log_b c .

More on log notation:

The equations  y = b x  and  x = log b y  say the same thing.

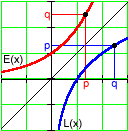Exponentials and logarithms are just different ways of expressing this relationship. The function  E(x) = b^x  asks for the value  y  that results when  b  is raised to the exponent  x . The function  L(x) = log_b x  asks for the exponent  y  for which  b^y  results in  x . The difference is: Which of  x  and  y  are you given and which do you wish to find? Which is the input and which is the output?

Consider:  2³ = 8 ,  log₂ 8 = 3 . The base is  2 . E(3) = 8 , L(8) = 3 .

This explains the "mirror image" relationship between exponentials and logarithms with the same base. If  (x, y)  is an input-output pair for one function, then  (y, x)  is an input-output pair for the other.

It also helps us to explain the meaning of the parameter  a . Since  b¹ = b , log_b(b) = 1 . That is, f(b) = a log_b b = a . The parameter  a  is the output when the input is the base. Nice, but not terribly useful...

It is better to think of  a  as a scaling factor, adjusting the outputs of  log_b(x)  up or down as  a  increases or decreases, respectively.

Laws of logarithms:

Because the base of a logarithm is really the base of an exponential in disguise, we carry over the restriction given for exponentials:

The base  b  in a logarithmic function must be positive.

For exponentials, this condition assured that outputs from  b^x  were always positive. For logarithms, this is a restriction that says the inputs must always be positive. Logarithms live entirely to the right of the y-axis. We say that they have a limited domain.

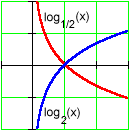
As with exponential functions, the base is responsible for a logarithmic function's rate of growth or decay.

• If  0 < b < 1 , the function decays as  x  increases. (E.g., log_1/2(1) > log_1/2(2) > log_1/2(3) .) Smaller values of  b  lead to slower rates of decay.
  
  
• If  b > 1 , the function grows as  x  increases. (E.g., log₂(1) < log₂(2) < log₂(3) .) Larger values of  b  lead to slower rates of growth.
  
  

The key algebraic property of logarithmic functions is the following.

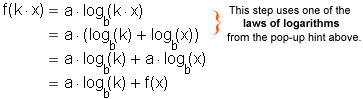
That is, multiplying any input  x  by a constant  k  results in adding a constant interval  a log_b(k)  to the output. This is once again the inverse of exponential behavior, where adding a constant interval to the input results in multiplying the output by a constant.

The property of input multiples producing equal output steps is the basis for many logarithmic scales used in applications.