Polynomial Functions

Algebraic Representation

f(x) = a n x n + a n – 1 x n – 1 + ... + a 2 x 2 + a 1 x + a 0

Polynomials are formed from sums of power functions – with one restriction. The restriction is that the powers must be non-negative integers – simple numbers like 0, 1, 2, 3, etc. This is some relief: The incredible variety among power functions, when powers are allowed to take on negative and fractional values, would lead to very complicated combined behaviors. By restricting the component power functions – the monomials or terms from which a polynomial is made – to non-negative integer exponents, polynomials become a family that is much easier to get to know.

Since an arbitrary number of power functions may be added together to form a polynomial, there is no limit to the number of parameters used in this family.

We generally call the parameters  a _k  that serve as scaling factors in the component power functions the coefficients of the polynomial. The coefficients can take on any real value (although we often add restrictions in practice).

The exponent  n  in the largest power is called the degree.

To understand the polynomials, it is convenient to start with the little ones. Like children marking their height on a doorpost, polynomials are known by the size of their degree. Here are a few of the elementary grades:

• n = 0. The constant polynomials: f(x) = a ₀
  
  Examples:
  
  
• n = 1. The linear polynomials: f(x) = a ₁ x + a ₀
  
  Examples:
  
  
• n = 2. The quadratic polynomials: f(x) = a ₂ x ² + a ₁ x + a ₀
  
  Examples:
  
  
• n = 3. The cubic polynomials: f(x) = a ₃ x ³ + a ₂ x ² + a ₁ x + a ₀
  
  Examples:
  
  
• n = 4. The quartic polynomials: f(x) = a ₄ x ⁴ + a ₃ x ³ + a ₂ x ² + a ₁ x + a ₀
  
  Examples:
  
  

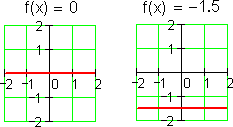
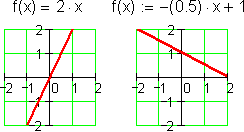
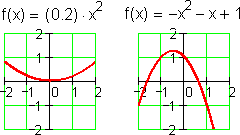
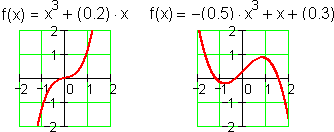
You can read more about the history of these elementary polynomials here.

As noted in the section on polynomial modeling, polynomial behavior is usually separated into its short and long term components. In the long term, polynomial behavior is very simple: It is dominated by the term of largest degree. In the short term, a polynomial may wiggle up and down, crossing the x-axis at various roots, and hitting highs and lows at various maxima and minima.

The algebra of polynomials has been studied for hundreds of years. Many important theorems about roots, maxima, and minima have accumulated. We explore a few of the most useful ones in the hints below.

  The Quadratic Formula

  The Factor Theorem

  The Fundamental Theorem of Algebra

  Descartes' Rule of Signs

  The Rational Root Theorem

  Maxima & Minima