Polynomial Functions

Modeling Representation

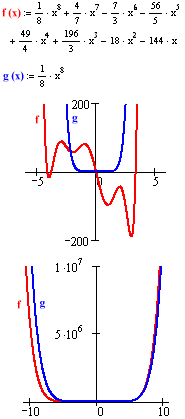
Polynomial functions are nothing more than a sum of power functions. As a result, certain properties of polynomials are very "power-like." When many different power functions are added together, however, polynomials begin to take on unique behaviors. To understand polynomial behavior, it is important to separate the long term from the short term. Long term behavior refers to what a polynomial does far from the origin – with inputs of large absolute value. Short term behavior refers to what a polynomial does close to the origin – with inputs of small absolute value. The terms "long," "short," "large," and "small," of course, are all relative. They depend very much on the particular polynomial. The long term behavior of a polynomial is very simple: It is indistinguishable from a single power function. A polynomial may be composed of many power functions, but one of these power functions always, eventually, dominates all of the others. The lesser power functions become insignificant by comparison, and the polynomial settles into the long term behavior of its dominant term. It is the short term behavior of polynomials that makes them most interesting. Near the origin, polynomials may wiggle up and down – crossing the x-axis at many roots and hitting many highs and lows – before the dominant power function can take long term control. The area around the origin is the polynomial party shack. All of a polynomial's exuberance is expressed here. It is this exuberant wiggling that ultimately distinguishes polynomials in modeling situations: Polynomial functions model data with multiple maxima and minima in the short term, and power trends in the long term.

Here are some places to look for a polynomial's peaks and valleys:

• The stock market. (price vs. time)
  
  
• Water levels in a resevoir. (height vs. time)
  
  
• Demand for electricity. (watts vs. time)
  
  
• The curves of a scalable computer font. (y vs. x)