Rational Functions

Algebraic Representation

f(x) = P(x) / Q(x)

A rational function is a quotient (ratio) of two polynomials  P  and  Q . To understand the behavior of rational functions, all you need to understand are ...quotients and polynomials!

Quotients (a.k.a. fractions) are simple enough: Just remember that the size of a quotient is proportional to the size of the numerator (P) and inversely proportional to the size of the denominator (Q).

Review of proportionality:

We use what we know about polynomials to understand the numerator and the denominator individually, then use what we know about fractions to understand the rational function as a whole.

Consider an example:

We factor both the numerator and the denominator (when possible) to get a look at the roots of  P  and  Q . We also like to expand both polynomials to see the terms of highest degree – the dominant terms. These are all we need to examine the short and long term behaviors, respectively, of the entire function.

When the numerator is zero, the entire quotient is zero (provided  Q  isn't zero at the same place): The roots of  P  are the roots of  f . In this case, P  and  f  have roots at  x = –2, 0, and  2 .

When the denominator is zero, the quotient is undefined: The roots of  Q  are the singularities of  f . In this case, f  has singularities at  x = –1  and  x = 1 .

When the input of  f  is near a singularity – when the denominator of the quotient is very small –  f  "blows up" in inverse proportion. Whether or not  f  travels through large positive or large negative values near a singularity depends on the relative signs of  P  and  Q  in that neighborhood. For example, to the left of  x = –1  both  P  and  Q  are positive, so their ratio is as well. The quotient blows up through large positive values. On the other side of  x = –1  Q  has turned negative while  P  remains positive. Their ratio is now negative and the quotient blows up through large negative values.

In the long term (far from the origin), both  P  and  Q  behave like their dominant terms. The quotient, therefore, behaves like the ratio of these terms. Suppose  P's  largest power is  a _m x ^m  and  Q's  largest power is  b _n x ⁿ . The ratio of these two terms is  (a _m/b _n) x ^{m – n} . We call this power function the asymptote of the rational function.

There are three possibilities:

• If  m > n , the asymptote is a positive power. Its long term behavior will depend on whether  m – n  is even or odd. (See section on power functions.)
  
  
• If  m = n , the asymptote is the constant  a _m/b _n . The function  f  approaches and "levels off" at this value in the long term. We say that the asymptote is horizontal.
  
  
• If  m < n , the asymptote is a negative power. The function  f  approaches zero and "levels off" along the x-axis in the long term. We say that the asymptote is horizontal.

In the example, the asymptote is  x ³/x ² , or simply  y = x . The function approaches the asymptote from below in the positive direction and from above in the negative direction. To see why this is so, we perform a long division:

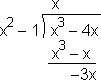
This tells us that:

Notice that, in the fraction being subtracted from  x , the denominator is always positive in the long term (|x| > 1). The numerator, on the other hand, is positive or negative depending on whether  x  is positive or negative, respectively. Thus, for large positive  x, the function actually has a little positive something subtracted from  x . For large negative  x , the function actually has a little negative something subtracted from (i.e. a little positive something added to)  x . This explains why  f(x) < x  for large positive  x  and  f(x) > x  for large negative  x .

The key algebraic properties of rational functions are simply the properties of fractions. You must know how changes in the numerator and the denominator affect the entire ratio. To understand the behaviors of the numerator and the denominator individually, of course, you must be familiar with the algebra of polynomials.