Rational Functions
Numeric Representation![]()
|
Certain algebraic properties distinguish rational functions from polynomials, and we can look for these in data sets to see if we should consider a rational model. One property of rational functions is the presence of singularities. In data, we can recognize a singularity by the very large output values, either positive or negative, in their immediate vicinity. Large values of opposite sign near the input Not all rational functions have singularities, however. For example, a data set modeled by the following function would not display any large output values:
|
Another property of rational functions is the presence of asymptotes. When a data set displays a recognizable horizontal asymptote, with outputs that "level off" at some fixed value, the behavior can not be described by a polynomial. Output values that level off at
Not all rational functions have horizontal asymptotes, however. If a data set has an underlying trend that is modeled by a rational function with a numerator of higher degree than the denominator, then the long term behavior will resemble a power function – just like a polynomial. For example, the function below becomes indistinguishable from the quadratic power
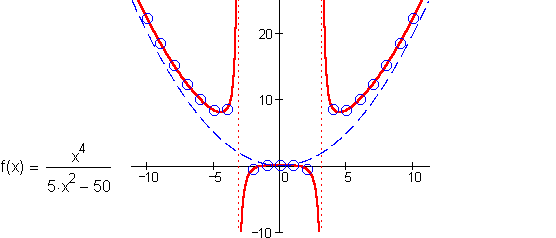
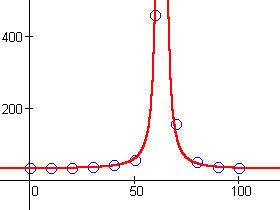
In the data for g above, something singular seems to occur between
We also notice that the data seems to level off around
If we graph
|
|
|
| Back to Contents | |