Trigonometric Functions

Modeling Representation

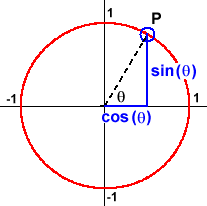Trigonometric functions are sometimes called circular functions. This is because the two fundamental trigonometric functions – the sine and the cosine – are defined as the coordinates of a point  P  travelling around on the unit circle of radius  1 .

As  P  moves around the circle of radius  1, the input variable – the angle  q  – changes. The outputs – cos(q) and sin(q) – give the  x  and  y  coordinates of  P, respectively.

Review of angular measure 

Methods for finding sines & cosines 

This gives us a clue about the kinds of phenomena that trigonometric functions are likely to model. Going around in a circle is a very simple kind of periodic behavior. Periodic behaviors repeat themselves at regular intervals. The sine and the cosine repeat their outputs at regular intervals. Indeed, each time  P  travels once around the circle (the input  q  changes by  2p  radians or 360º) the coordinates of  P  (the outputs of sine and cosine) repeat.

By changing the size of the circle and the speed at which the point  P  travels around it, transformations of the sine and the cosine can be made to model a wide variety of regularly repeating behaviors.

Trigonometric functions model data with periodic trends.

Here are some situtations that should make you think of trigonometric functions:

• A ferris wheel. (horizontal and vertical distance vs. angle)
  
  
• A hula dancer. (horizontal and vertical distance vs. angle)
  
  
• The length of daylight. (length vs. day of the year)
  
  
  
• The changing seasons. (temperature vs. day of the year)
  
  
• A repetitious calculation. (step vs. time)

Words and phrases like "seasonal," "repeatedly," and "over and over" usually indicate the presence of trigonometric functions.