Trigonometric Functions

Algebraic Representation

f(x) = a sin [b (x + c)] + d

Members of this family have four parameters to change when shaping themselves to model periodic phenomena:

• a  is called the amplitude or the vertical dilation.
  
  
• b  is called the horizontal dilation.
  
  
• c  is called the phase shift or the horizontal translation.
  
  
• d  is called the vertical translation.

The dilations also have informal names. When  |a| < 1  or  |b| > 1 , they are called crunches. When  |a| > 1  or  |b| < 1 , they are called stretches.

The meaning of these suggestive terms is most apparent when looking at the graphs of the trigonometric functions. With so many parameters to "tune," however, it is clear that this family has great algebraic flexibility.

The key algebraic property of the sine and the cosine functions is their periodicity:

sin (q ± 2kp) = sin (q)

cos (q ± 2kp) = cos (q)

That is, adding or subtracting any angle of  2kp  radians (k  times around the circle) to or from any angle  q  takes us back to the same point on the circle, the same  y  and  x  coordinates, and the same sine and cosine. Said another way, if we know the values of these functions for  q  between  0  and  2p, then we know the values for any  q .

The length of the shortest input interval containing all of the information about a periodic function is called the period. Both the sine and the cosine have periods of  2p .

Another important algebraic property of trigonometric functions is the relationship between the sine and the cosine. Their behavior is very similar. In fact, each time we change our position on the unit circle by  p/2  radians (90º), the  x  and  y  coordinates simply reverse themselves, while one of them changes sign:

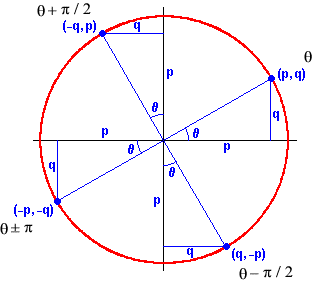
We see that:

p = cos(q) = sin(q + p/2) = –sin(q – p/2) = –cos(q ± p)

and that:

q = sin(q) = –cos(q + p/2) = cos(q – p/2) = –sin(q ± p)

These relationships are examples of trigonometric identities. Identities give us equivalent ways of saying identical things. In particular, the identity  cos(q) = sin(q + p/2)  tells us that the cosine function is identical to a sine function with a phase shift of  p/2 . This is why we are able to work exclusively with the sine function when modeling periodic phenomena: The cosine doesn't add anything new.

There are many other useful identities related to the sine and cosine functions. Like the identities above, they come from observing the many pleasing symmetries of the circle.

More trig identities 

There are other trigonometric functions that are sometimes used in applications. All of them, however, are simple ratios of the sine and cosine. Just as we understand rational functions by observing the behavior of the polynomials in their numerators and denominators, so the remaining trigonometric functions can be understood in terms of the basic behaviors of the sine and cosine.

Meet the other trig functions 

The trigonometric functions have been around for a long time. Their origins, however, were not in the study of periodic phenomena. Rather, early trigonometry concerned itself with the ratios found in right triangles. (Greek roots: tri, three + gonia, angle + metria, measure.) Even if it has little to do with modeling, the subject is still eminently practical.

Introduction to triangle trigonometry 

If you'd like to learn more about the long history of the trigonometric functions, go here.