Logistic Functions

Modeling Representation

Logistic functions combine, in one neat package, two characteristic kinds of exponential growth:

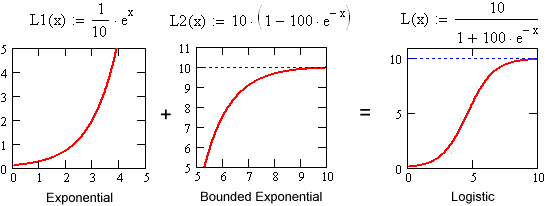
The first kind of exponential growth is the familiar pattern of increase at an increasing rate. Since the growth is exponential, the growth rate is actually proportional to the size of the function's value.

The second kind of exponential growth is usually called bounded exponential growth. It's really just a clever trick: It takes a decaying exponential and subtracts it from a fixed bound. As the decaying exponential dies out, the difference rises up to the bound. This kind of function models growth that is limited by some fixed capacity.

Logistic functions combine the first kind of exponential growth, when the outputs are small, with the second kind of exponential growth, when the outputs near capacity:

Logistic functions model resource limited exponential growth.

Look for the logistic function's characteristic "S" shape in situations such as:

• Island populations.
  
  
• Bacteria in a petri dish.
  
  
• Growth of seedlings.
  
  
• Accumulation of a function with a peak value.