Logistic Functions
Algebraic Representation![]()
|
f(x) = a / (1 + b c –x) |
The algebra of the logistic family is something of a hybrid. It mixes together the behaviors of both exponentials and powers (proportions, like rational functions).
The study of logistic functions, therefore, begins to lead us away from the truly fundamental families of functions and into the larger world where descriptions of complex phenomena are composed of many functions. The logistic family's characteristic behavior appears often enough in applications, however, that it is worth examining in its own right.
The three parameters of the logistic family work together to produce its characteristic behavior, and they are best understood in combination.
The parameters b and c are simply the y-intercept and the base of the component exponential function
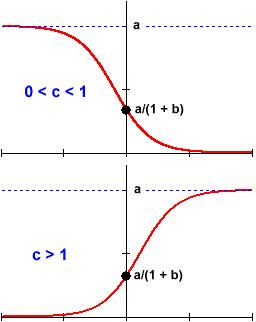 The significance of the parameter a depends on the behavior of this exponential function. In the short term, when x is near 0 and
The significance of the parameter a depends on the behavior of this exponential function. In the short term, when x is near 0 and
It is this latter behavior, in which the function rises up to and eventually levels off at a constant horizontal asymptote, that is most often seen in models of "resource-limited" growth. Indeed, the function never exceeds the value a . Thus, the parameter a is often called the limiting value or, in the description of populations, the carrying capacity.
The rate at which a logistic function falls from or rises to its limiting value is completely determined by the exponential function in the denominator. In particular, by the paramenters b and c .
In the case of decay
The change-over from a precipitous decrease or increase to the beginnings of an eventual levelling-off always occurs half-way up or down the logistic curve. This point of critical change in the function's behavior is called the inflection point.
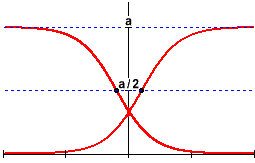
Using this information (which comes from calculus), we can calculate the inflection point's exact location:
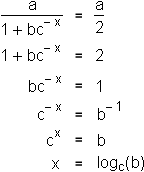
|
|
|
| Back to Contents | |