The Rational Root Theorem

Theorem: If the polynomial P(x) = a n x n + a n – 1 x n – 1 + ... + a 2 x 2 + a 1 x + a 0 has any rational roots, then they must be of the form

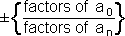
The importance of the Rational Root Theorem is that it lets us know which roots we may find exactly (the rational ones) and which roots we may only approximate (the irrational ones).

Here is how it works.

Consider the polynomial

P(x) = x ³ – 8 x ² + 17 x – 10

In this case, a ₀ = –10  and a _n = 1 . The number  –10  has factors of   {10, 5, 2, 1} . The number  1  has factors of   1 . Thus, if  P  has any rational roots at all, they must be among   {10/1, 5/1, 2/1, 1/1} = {10, 5, 2, 1} . In fact, a quick check shows that  5, 2, and  1  are all rational (actually integer) roots.

Consider, instead,

f(x) = 2 x ³ + 3 x ² + 2 x + 3

In this case, a ₀ = 3  and a _n = 2 . The number  3  has factors of   {3, 1} . The number  2  has factors of   {2, 1} . Thus, if  f  has any rational roots at all, they must be among   {3/1, 1/1, 3/2, 1/2} . Of the eight (positive and negative) possibilities, only  –3/2  is a root. If we now use the Factor Theorem and factor out  (x + 3/2) , we get  f(x) = (x + 3/2)(2 x ² + 2) . The Quadratic Formula shows us that there are no further (necessarily irrational) roots of the quotient polynomial  2 x ² + 2 .

Finally, consider

g(x) = x ³ – x ² + 1

Descartes' Rule of Signs tells us that  g  has at most one negative root, and a quick graph shows the function crossing the x-axis somewhere between  –1  and  0 . The possibilities given by the Rational Root Theorem  ( 1)  don't fit the bill. We conclude that this root must be irrational. Bracketing or zooming gives an approximate value of  –0.755 .