You may have noticed something, however: Starting with any set of data, we can always draw a curve – in fact, lots of curves – that "connect the dots" and fit the data perfectly. The sum of the squares of the residuals will be zero. So what's all the fuss?
There are at least two problems with simply "connecting the dots." One is that a curve that fits every bump in the data may have a quite complicated equation. The second is that all of those bumps, as we have noted, may be due to noise or experimental error, and not genuine trends in the data. What we want is an equation with a simple description that follows the data's general trend while ignoring the noisy bumps. This takes just a little fuss.
But not much. All we have to do is agree on what a "simple description" will be. This means picking a functional form from among some simple families of functions:
-
 linear functions, of the form y = a + bx . linear functions, of the form y = a + bx .
-
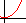 power functions, of the form y = a x b + c . power functions, of the form y = a x b + c .
-
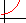 exponential functions, of the form y = a b x + c . exponential functions, of the form y = a b x + c .
-
 logarithmic functions, of the form y = a log(x + b) + c . logarithmic functions, of the form y = a log(x + b) + c .
-
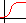 logistic functions, of the form y = a / (1 + b e –cx) . logistic functions, of the form y = a / (1 + b e –cx) .
-
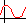 trigonometric functions, of the form y = a sin[b (x + c)] + d . trigonometric functions, of the form y = a sin[b (x + c)] + d .
|
This is why a plot of the data is such an important first step: We look for a general trend in the data "by eye" and then pick a family with the same general trend. The method of least squares adjusts the parameters a, b, c, and d in a family's description until it finds the one family member for which the sum of the squares of the residuals is as small as possible.
How the method of least squares chooses the "best" a, b, c, and d, from among all of the possible choices, alas, is a matter for calculus. For now, we will trust the computer to carry out the method accurately and efficiently for us.
This doesn't absolve us from the responsibility of first picking a reasonable family to fit the data's trend. The method of least squares will only optimize a curve within a given family.
This general procedure for finding an equation to describe a set of data points is called parametric fitting. It is a particular kind of regression analysis. (General regression analyses vary not only the parameters, but the functional family.) Here's a review of the steps:
- Plot the data and look for a general trend.
- Pick a family of functions with a simple equation that will follow the same general trend.
- Adjust the parameters in the family to find a particular fitting function for which the sum of the squares of the residuals is as small as possible.
- Use the method of least squares to optimize the last step and find the absolute "best" fitting function from the chosen family.
- Use the best fitting function to interpolate and extrapolate values outside of the data.
 linear functions, of the form
linear functions, of the form  power functions, of the form
power functions, of the form  exponential functions, of the form
exponential functions, of the form  logarithmic functions, of the form
logarithmic functions, of the form  logistic functions, of the form
logistic functions, of the form  trigonometric functions, of the form
trigonometric functions, of the form