Example 4: Exchange Rates

Click here to open an associated Mathcad worksheet:

Travelers arriving at Heathrow Airport in London have the opportunity to exchange their dollars ($) for pounds (£). Imagine that you arrive with  x  dollars to exchange.

The number of pounds  y  you will receive in return will be some multiple,  rx, of the number of dollars, with  0 < r < 1  (since each dollar will buy less than one pound). The multiple  r  is called the exchange rate, given in pounds per dollar, and it varies from day to day.

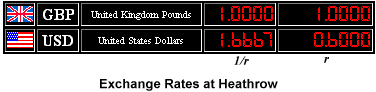
At any particular time the exchange rate is fixed, and the exchange function  y = E(x) = rx  is linear: increasing at a constant rate as you exchange more dollars for more pounds. A graph of pounds versus dollars for the time you arrive might look like this:

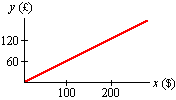
You can see that 100 dollars will buy 60 pounds, 200 dollars will buy 120 pounds, and the exchange rate is at  r = 60/100 = 120/200 = 0.6000  pounds per dollar.

What about the changing exchange rate? We can't picture it as a concavity in this plot. The reason is that the exchange rate varies with time, not  x, and we have no way to plot time on a graph of  y  vs.  x.

We could do the following, however:

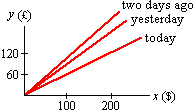
Now we can see that the exchange rate (slope of the line) is decreasing with time, and apparently decreasing at an increasing absolute rate. A plot of  r  vs.  t  might look like this:

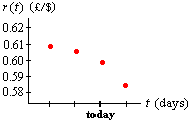
You'd better sell those dollars today!