Example 3: Velocity of an Oil Drop
Example 3: Velocity of an Oil Drop |
Click here to open an associated Mathcad worksheet: |
Physicists have found that the velocity of an oil drop, when falling through a vacuum, is well-described by the formula:
![]()
where v0 is the drop's initial downward velocity (say, when it breaks free as a drip) and g is the "constant acceleration due to gravity," fixed at about
The velocity is a rate of change, measuring the rate at which the drop's distance above the ground x(t) (in feet) is decreasing. We have seen that decreasing functions have negative rates of change, and so the velocities in this example will all be negative numbers. Since the constant g is also negative, the formula shows that the velocities become more and more negative as time goes on, just as we would expect of a freely falling object. The absolute values of the velocities (the speeds) thus become greater.
The function x(t), which is decreasing at an increasing (absolute) rate, is concave down. A plot of x(t), for a drop beginning 1 ft above the ground with an initial downward velocity of
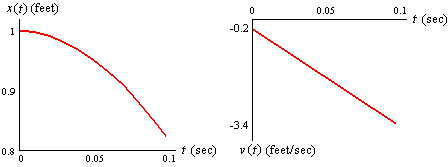
|
|
|
| Back to Contents | |