| Transformations
|
Click here to open an associated Mathcad worksheet: 
|
One simple way to create a new function from an old one is to add an adjustable parameter a . We call these modifications transformations of the given rule.
Suppose we are given a function f by a rule y = f(x) which is described verbally, algebraically, graphically, or numerically. There are some obvious ways to alter the rule by adding an adjustable parameter a :
-
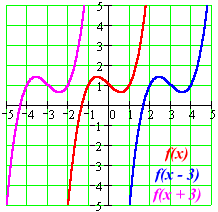
The parameter a can be added to or subtracted from the input x before the rule f is applied:
y = f(x) becomes y = f(x ± a)
These transformations are called horizontal shifts or translations. They move the graph of the given function left (adding positive a) or right (subtracting positive a).
|
|
-
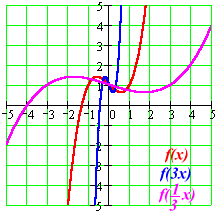
The parameter a can multiply the input x before the rule f is applied:
y = f(x) becomes y = f(ax)
These transformations are called horizontal stretches, crunches or dilations. They horizontally stretch (a < 1) or squeeze (a > 1) the graph of the given function.
|
|
-
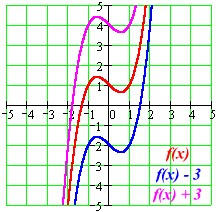
The parameter a can be added to or subtracted from the output y after the rule f is applied:
y = f(x) becomes y = f(x) ± a
These transformations are called vertical shifts or translations. They move the graph of the given function up (adding positive a) or down (subtracting positive a).
|
|
-
The parameter a can multiply the output y after the rule f is applied:
y = f(x) becomes y = af(x)
These transformations are called vertical stretches, crunches or dilations. They vertically stretch (a > 1) or squeeze (a < 1) the graph of the given function.
|

|
These basic transformations allow you to "work a function into shape". If you begin with a "known" function of approximately the right form, transformations — singly or in combination — add the adjustable parameters that let you fine-tune the form, as necessary, to fit a particular modeling situation.



